II Arbitrarily Large Data

9 Lists

Structures are useful when you know exactly how many pieces of information you wish to represent as a single piece of data. Even if you create deeply nested structures according to the data definitions of Fixed-Size Data, you always know exactly how many atomic pieces of data it contains. Many programming problems, though, deal with an undetermined number of pieces of information that must be processed as one piece of data. For example, an advanced thermostat may record a series of temperature recordings and your program may have to compute some form of average. Or, you may wish to allow the player in the space invader game to fire many shots, in which case the world state must keep track of all of these shots. With what you know, however, it is impossible to formulate a data definition that can represent this kind of state of the world.

To tackle problems that require representations of arbitrarily large but still finite pieces of information, we need a new way to formulate data definitions. In this chapter, we introduce these self-referential data definitions and one important example—lists—and we explore how to design programs based on self-referential data definitions. So that you realize that lists are just one example for this new way of defining data, later chapters in this part of the book illustrate the idea with a variety of examples. Intertwined Data generalizes this data-definition mechanism yet again.

9.1 Creating Lists

All of us make lists all the time. Before we go grocery shopping, we write down a list of items we wish to purchase. Some people write down a to-do list every morning. During December, many children prepare Christmas wish lists. To plan a party, we make a list of invitees. Arranging information in the form of lists is a ubiquitous part of our life.

Given that information comes in the shape of lists, we must clearly learn how to represent such lists as BSL data. Indeed, because lists are so important BSL comes with built-in support for creating and manipulating lists, similar to the support for Cartesian points (posn). In contrast to points, the data definition for lists is always left to you. But first things first. We start with the creation of lists.

When we form a list, we always start out with the empty list. In BSL, we represent the empty list with

empty

which, like true or 5, is just a constant. When we add something to a list, we construct another list; in BSL, the cons operation serves this purpose. For example,

(cons "Mercury" empty)

constructs a list from the empty list and the string "Mercury". Figure 31 presents this list in the same pictorial manner we used for structures. The box for cons has two fields: first and rest. In this specific example the first field contains "Mercury" and the rest field contains empty.

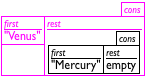
(cons "Mercury"
      empty)
(cons "Venus"
      (cons "Mercury"
            empty))
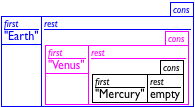
(cons "Earth"
      (cons "Venus"
            (cons "Mercury"
                  empty)))
Figure 31: Building a list

Once we have a list with one item in it, we can construct lists with two items by using cons again. Here is one:

(cons "Venus" (cons "Mercury" empty))

And here is another:

(cons "Earth" (cons "Mercury" empty))

The middle row of figure 31 shows how you can imagine lists that contain two items. It is also a box of two fields, but this time the rest field contains a box. Indeed, it contains the box from the top row of the same figure.

Finally, we construct a list with three items:

(cons "Earth" (cons "Venus" (cons "Mercury" empty)))

The last row of figure 31 illustrates the list with three items. Its rest field contains a box that contains a box again. So, as we create lists we put boxes into boxes into boxes, etc. While this may appear strange at first glance, it is just like a set of Chinese gift boxes or a set of nested drinking cups, which we sometimes get for birthdays. The only difference is that BSL programs can nest lists much deeper than any artist could nest physical boxes.

(cons "Earth"
      (cons "Venus"
            (cons "Mercury"
                  empty)))

Figure 32: Drawing a list

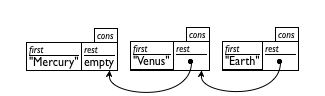
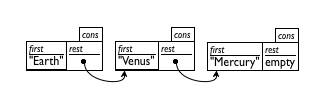
Because even good artists would have problems with drawing deeply nested structures, computer scientists resort to box-and-arrow diagrams instead. Figure 32 illustrates how to re-arrange the last row of figure 31. Each cons structure becomes a separate box. If the rest field is too complex to be drawn inside of the box, we draw a bullet instead and a line with an arrow to the box that it contains. Depending on how the boxes are arranged you get two kinds of diagrams. The first, displayed in the top row of figure 32, lists the boxes in the order in which they are created. The second, displayed in the bottom row, lists the boxes in the order in which they are consed together. Hence the second diagram immediately tells you what first would produced when applied to the list, no matter how long the list is. For this reason, people tend to prefer the second arrangement.

Exercise 118. Create BSL lists that represent
a list of celestial bodies, say, at least all the planets in our solar system;
a list of items for a meal, for example, steak, French fries, beans, bread, water, brie cheese, and ice cream; and
a list of colors.
Sketch box representations of these lists, similar to those in figure 31 and figure 32. Which of the sketches do you like better?

You can also make lists of numbers. As before, empty is the list without any items. Here is a list with the 10 digits:

(cons 0
  (cons 1
    (cons 2
      (cons 3
        (cons 4
          (cons 5
            (cons 6
              (cons 7
                (cons 8
                  (cons 9 empty))))))))))

To build this list requires 10 list constructions and one empty. For a list of three arbitrary numbers, for example,

(cons pi
(cons e
(cons -22.3 empty)))

we need three conses.

In general a list does not have to contain values of one kind, but may contain arbitrary values:

(cons "Robbie Round"
  (cons 3
    (cons true
      empty)))

Then again, if this list is supposed to represent a record with a fixed number of pieces, use a structure type instead. The first item of this list is a string, the second one is a number, and the last one a Boolean. You may consider this list as the representation of a personnel record with three pieces of data: the name of the employee, the number of years spent at the company, and whether the employee has health insurance through the company. Or, you could think of it as representing a virtual player in some game. Without a data definition, you just can’t know what data is all about.

Here is a first data definition that involves cons:

; A 3LON is (cons Number (cons Number (cons Number empty)))
; interp. (cons 1 (cons -1 (cons -2 empty))) represents a point
; in a three-dimensional space

Of course, this data definition uses cons like others use constructors for structure instances, and in a sense, cons is just a special constructor. What this data definition fails to demonstrate is how to form lists of arbitrary length: lists that contain nothing, one item, two items, ten items, or perhaps 1,438,901 items.

So let’s try again:

; A List-of-names is one of:
; – empty
; – (cons String List-of-names)
; interp. a List-of-names represents a list of invitees by last name

Stop. Take a deep breath, and read it again. This data definition is one of the most unusual definitions you have ever encountered—where else have you seen a definition that refers to itself?—and it isn’t even clear whether it makes sense. After all, if you had told your English teacher that “a table is a table” defines the word “table,” the most likely response would have been “Nonsense!” because a self-referential definition doesn’t explain what a word means.

In computer science and in programming, though, self-referential definitions play a central role, and with some care, such definitions actually do make sense. Here “making sense” means that we can use the data definition for what it is intended for, namely, to generate examples of data that belong to the class that is being defined or to check whether some given piece of data belongs to the defined class of data. From this perspective, the definition of List-of-names makes complete sense. At a minimum, we can generate the empty list as one example, using the first clause in the itemization. Given empty as an element of List-of-names, it is also easy to make a second example:

(cons "Findler" empty)

Here we are using a String and the only list from List-of-names to generate a piece of data according to the second clause in the itemization. With the same rule, we can generate many more lists of this kind:

(cons "Flatt" empty)
(cons "Felleisen" empty)
(cons "Krishnamurthi" empty)

And while these lists all contain one name (represented as a String), it is actually possible to use the second line of the data definition to create lists with more names in them:

(cons "Felleisen" (cons "Findler" empty))

This piece of data belongs to List-of-names because "Felleisen" is a String and (cons "Findler" empty) is a List-of-names according to our argument above.

Exercise 119. Create an element of List-of-names that contains five Strings. Sketch a box representation of the list similar to those found in figure 31.
Explain why
(cons "1" (cons "2" empty))
is an element of List-of-names and why (cons 2 empty) isn’t.

Now that we know why our first self-referential data definition makes sense, let us take another look at the definition itself. Looking back we see that all the original examples in this section fall into one of two categories: start with an empty list or use cons to add something to an existing list. The trick then is to say what kind of “existing lists” you wish to allow, and a self-referential definition ensures that you are not restricted to lists of some fixed length.

Exercise 120. Provide a data definition for representing lists of Boolean values. The class contains all arbitrarily long lists of Booleans.

9.2 What Is empty, What Is cons

Let us step back for a moment and take a close look at empty and cons. As mentioned, empty is just a constant. When compared to constants such as 5 or "this is a string", it looks more like a function name or a variable; but when compared with true and false, it should be easy to see that it really is just BSL’s representation for empty lists.

The one question left is to which class of values empty belongs. It clearly isn’t a number, a Boolean, a string, or anything other form of atomic data. It also isn’t a piece of compound data, such as Posns or other structure types we have defined. Instead, empty is a singular kind of value and it belongs into a class all by itself. As such, this class of values comes with a predicate that recognizes only empty and nothing else:

; Any -> Boolean
; is the given value empty or not?
(define (empty? x) ...)

Like all class predicates, empty? can be applied to any value from the universe of BSL values. It produces true, however, only if it is applied to empty. Thus,

> (empty? empty)
true
> (empty? 5)
false
> (empty? "hello world")
false
> (empty? (cons 1 empty))
false
> (empty? (make-posn 0 0))
false

Everything we have seen so far suggests that cons is a constructor just like those introduced by structure type definitions. More precisely, cons appears to be the constructor for a two-field structure, the first one for the additional element and the second one for the already-existing list. The following definitions translate this idea into code:

(define-struct combination (left right))
; A ConsCombination is (make-combination Any Any).

; Any Any -> ConsCombination
(define (our-cons a-value a-list)
(make-combination a-value a-list))

The only catch is that our-cons accepts all possible BSL values for its second argument and cons doesn’t, as the following experiment validates:

> (cons 1 2)
cons: second argument must be a list, but received 1 and 2

Put differently, cons is really a checked function, the kind discussed in Itemizations and Structures, which suggests the following refinement:

; A ConsOrEmpty is one of:
; – empty
; – (cons Any ConsOrEmpty)
; interp. ConsOrEmpty is the class of all BSL lists

; Any ConsOrEmpty -> ConsOrEmpty
(define (our-cons a-value a-list)
  (cond
    [(empty? a-list) (make-combination a-value a-list)]
    [(our-cons? a-list) (make-combination a-value a-list)]
    [else (error "cons: list as second argument expected")]))

If cons is a checked constructor function, you may be wondering how to extract the pieces from the resulting structure. After all, Adding Structure says that programming with structures requires selectors. Since a cons structure has two fields, there are two selectors: first and rest. They are also easily defined in terms of our combination structure:

; ConsOrEmpty -> Any
; extract the left part of the given combination
(define (our-first a-combination)
  (combination-left a-combination))

; ConsOrEmpty -> Any
; extract the right part of the given combination
(define (our-rest a-combination)
  (combination-right a-combination))

; Any -> Boolean
; is the given value an instance of the combination structure?
(define (our-cons? x)
  (combination? x))

If the structure type definition for combination were available, it would be easy to create combinations that don’t contain empty or another combination in the right field. Whether such bad instances are created intentionally or accidentally, they tend to break functions and programs in strange ways. So the actual structure type definition underlying cons remains hidden to avoid problems. Local Function Definitions demonstrates how you can hide definitions, too, but for now, you don’t need this power.

empty
--- a special value, mostly to represent the empty list
empty?
--- a predicate to recognize empty and nothing else
cons
--- a checked constructor to create two-field instances
first
--- the selector to extract the last item added
rest
--- the selector to extract the extended list
cons?
--- a predicate to recognizes instances of cons
Figure 33: List primitives

Figure 33 summarizes all this. The key insight is that cons is a checked constructor and that first, rest, and cons? are merely distinct names for the usual predicate and selectors. What this chapter teaches then is not a new way of creating data but a new way of formulating data definitions.

9.3 Programming With Lists

Say you’re keeping track of your friends with some list, and say the list has grown so large that you need a program to determine whether some specific name is on the list. To make this idea concrete, let us state it as an exercise:

Sample Problem: You are working on the contact list for some new cell phone. The phone’s owner updates—adds and deletes names—and consults this list—looks for specific names—on various occasions. For now, you are assigned the task of designing a function that consumes this list of contacts and determines whether it contains the name “Flatt.”

We will solve this problem here, and once we have a solution to this sample problem, we will generalize it to a function that finds any name on a list.

The data definition for List-of-names from the preceding is appropriate for representing the list of names that the function is to search. Next we turn to the header material:

; List-of-names -> Boolean
; to determine whether "Flatt" occurs on a-list-of-names
(define (contains-flatt? a-list-of-names)
false)

Following the general design recipe, we next make up some examples that illustrate the purpose of contains-flatt?. First, we determine the output for the simplest input: empty. Since this list does not contain any strings, it certainly does not contain "Flatt", and the expected answer is false:

(check-expect (contains-flatt? empty) false)

Then we consider lists with a single item. Here are two examples:

(check-expect (contains-flatt? (cons "Findler" empty)) false)
(check-expect (contains-flatt? (cons "Flatt" empty)) true)

In the first case, the answer is false because the single item on the list is not "Flatt"; in the second case, the item is "Flatt", and the answer is true. Finally, here are two more general examples, with lists of several items:

(check-expect
  (contains-flatt? (cons "Mur" (cons "Fish"  (cons "Find" empty))))
  false)
(check-expect
  (contains-flatt? (cons "A" (cons "Flatt" (cons "C" empty))))
  true)

Again, the answer in the first case must be false because the list does not contain "Flatt", and in the second case it must be true because "Flatt" is one of the items on the list provided to the function.

Take a breath. Run the program. The header is a “dummy” definition for the function; you have some examples; they have been turned into tests; and best of all, some of them actually succeed. They succeed for the wrong reason but succeed they do. If things make sense now, read on.

The fourth step is to design a function template that matches the data definition. Since the data definition for lists of strings has two clauses, the function’s body must be a cond expression with two clauses. The two conditions—(empty? a-list-of-names) and (cons? a-list-of-names)—determine which of the two kinds of lists the function received:

(define (contains-flatt? a-list-of-names)
  (cond
    [(empty? a-list-of-names) ...]
    [(cons? a-list-of-names) ...]))

Instead of (cons? a-list-of-names), we could use else in the second clause.

We can add one more hint to the template by studying each clause of the cond expression in turn. Specifically, recall that the design recipe suggests annotating each clause with selector expressions if the corresponding class of inputs consists of compounds. In our case, we know that empty does not have compounds, so there are no components. Otherwise the list is constructed from a string and another list of strings, and we remind ourselves of this fact by adding (first a-list-of-names) and (rest a-list-of-names) to the template:

(define (contains-flatt? a-list-of-names)
  (cond
    [(empty? a-list-of-names) ...]
    [(cons? a-list-of-names)
     (... (first a-list-of-names) ... (rest a-list-of-names) ...)]))

Now it is time to switch to the programming task proper, the fifth step of our design recipe. It starts from template and deals with each cond-clause separately. If (empty? a-list-of-names) is true, the input is the empty list, in which case the function must produce the result false. In the second case, (cons? a-list-of-names) is true. The annotations in the template remind us that there is a first string and the rest of the list. So let us consider an example that falls into this category:

(cons "A"
(cons ...
... empty))

The function, just like a human being, must clearly compare the first item with "Flatt". In this example, the first string is "A" and not "Flatt", so the comparison yields false. If we had considered some other example instead, say,

(cons "Flatt"
(cons ...
... empty))

the function would determine that the first item on the input is "Flatt", and would therefore respond with true. All of this implies that the second line in the cond expression should contain an expression that compares the first name on the list with "Flatt":

(define (contains-flatt? a-list-of-names)
  (cond
    [(empty? a-list-of-names) false]
    [(cons? a-list-of-names)
     (... (string=? (first a-list-of-names) "Flatt") ...
      ... (rest a-list-of-names) ...)]))

Furthermore, if the comparison of (first a-list-of-names) yields true, the function is done and produces true. If the comparison yields false, we are left with another list of strings: (rest a-list-of-names). Clearly, we can’t know the final answer in this case, because depending on what “...” represents, the function must produce true or false. Put differently, if the first item is not "Flatt", we need some way to check whether the rest of the list contains "Flatt".

Fortunately, we have just such a function: contains-flatt?, which according to its purpose statement determines whether a list contains "Flatt". The purpose statement implies that if l is a list of strings, (contains-flatt? l) tells us whether l contains the string "Flatt". Similarly, (contains-flatt? (rest l)) determines whether the rest of l contains "Flatt". And in the same vein, (contains-flatt? (rest a-list-of-names)) determines whether or not "Flatt" is in (rest a-list-of-names), which is precisely what we need to know now.

In short, the last line of the function should be (contains-flatt? (rest a-list-of-names)):

; List-of-names -> Boolean
(define (contains-flatt? a-list-of-names)
  (cond
    [(empty? a-list-of-names) false]
    [(cons? a-list-of-names)
     (... (string=? (first a-list-of-names) "Flatt") ...
      ... (contains-flatt? (rest a-list-of-names)) ...)]))

The trick is now to combine the values of the two expressions in the appropriate manner. As mentioned, if the first expression yields true, there is no need to search the rest of the list; if it is false, though, the second expression may still yield true, meaning the name "Flatt" is on the rest of the list. All of this suggests that the result of (contains-flatt? a-list-of-names) is true if either the first expression in the last line or the second expression yields true.

; List-of-names -> Boolean
; to determine whether "Flatt" occurs on a-list-of-names

(check-expect
  (contains-flatt? (cons "Mur" (cons "Fish"  (cons "Find" empty))))
  false)
(check-expect
  (contains-flatt? (cons "A" (cons "Flatt" (cons "C" empty))))
  true)

(define (contains-flatt? a-list-of-names)
  (cond
    [(empty? a-list-of-names) false]
    [(cons? a-list-of-names)
     (or (string=? (first a-list-of-names) "Flatt")
         (contains-flatt? (rest a-list-of-names)))]))
Figure 34: Searching a list

Here then is the complete definition: figure 34. Overall it doesn’t look too different from the definitions in the first chapter of the book. It consists of a signature, a purpose statement, two examples, and a definition. The only way in which this function definition differs from anything you have seen before is the self-reference, that is, the reference to contains-flatt? in the body of the define. Then again, the data definition is self-referential, too, so in some sense this second self-reference shouldn’t be too surprising.

Exercise 121. Use DrRacket to run contains-flatt? in this example:
(cons "Fagan"
  (cons "Findler"
    (cons "Fisler"
      (cons "Flanagan"
        (cons "Flatt"
          (cons "Felleisen"
            (cons "Friedman" empty)))))))
What answer do you expect?

Exercise 122. Here is another way of formulating the second cond clause in contains-flatt?:
... (cond
[(string=? (first a-list-of-names) "Flatt") true]
[else (contains-flatt? (rest a-list-of-names))]) ...
Explain why this expression produces the same answers as the or expression in the version of figure 34. Which version is better? Explain.

Exercise 123. Develop the function contains?, which determines whether some given string occurs on a list of strings.

10 Designing With Self-Referential Data Definitions

At first glance, self-referential data definitions seem to be far more complex than those for compound or mixed data. But, as the example of contains-flatt? shows, the six steps of the design recipe still work. Nevertheless, in this section we discuss a new design recipe that works better for self-referential data definitions. As implied by the preceding section, the new recipe generalizes those for compound and mixed data. The new parts concern the process of discovering when a self-referential data definition is needed, deriving a template, and defining the function body:

If a problem statement discusses compound information of arbitrary size, you need a self-referential data definition. At this point, you have seen only one such class, List-of-names, but it is easy to see that it defines the collection of lists of strings, and it is also easy to imagine lists of numbers, etc.
Numbers also seem to be arbitrarily large. For inexact numbers, this is an illusion. For precise integers, this is indeed the case. Dealing with integers is therefore a part of this chapter.
For a self-referential data definition to be valid, it must satisfy two conditions. First, it must contain at least two clauses. Second, at least one of the clauses must not refer back to the class of data that is being defined. It is therefore good practice to identify the self-references explicitly with arrows from the references in the data definition back to its beginning.
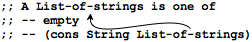
Figure 35: Arrows for self-references in data definitions
You can, and should, also check the validity of self-referential data definitions with the creation of examples. If it is impossible to generate examples from the data definition, it is invalid. If you can generate examples but you can’t see how to generate larger and larger examples, the definition may not live up to its interpretation.
Nothing changes about the header material. You still need a signature, a purpose statement, and a dummy definition. When you do formulate the purpose statement, it is as important as always to keep in mind that it should specify what the function computes not how it goes about it, especially not how it goes through instances of the given data.
Be sure to work through input examples that use the self-referential clause of the data definition several times. It is the best way to formulate tests that cover the entire function definition later.

At the core, a self-referential data definition looks like a data definition for mixed data. The development of the template can therefore proceed according to the recipe in Itemizations and Structures. Specifically, we formulate a cond expression with as many cond clauses as there are clauses in the data definition, match each recognizing condition to the corresponding clause in the data definition, and write down appropriate selector expressions in all cond lines that process compound values.

Does the data definition distinguish among different subclasses of data?
Your template needs as many cond clauses as subclasses that the data definition distinguishes.
How do the subclasses differ from each other?
Use the differences to formulate a condition per clause.
Do any of the clauses deal with structured values?
If so, add appropriate selector expressions to the clause.
Does the data definition use self-references?
Formulate ``natural recursions'' for the template to represent the self-references of the data definition.
Some data definitions refer to others. For those, use this advice:
Does the data definition refer to another data definition?
Contemplate the development of a separate template. See Structures In Lists.
Figure 36: How to translate a data definition into a template

Figure 36 expresses this idea as a “question and answer” game. In the left column it states questions you need to ask about the data definition for the argument, and in the right column it explains what the answer means for the construction of the template. If you ignore the last row and apply the first three questions to any function that consumes a List-of-strings, you arrive at this shape:

(define (fun-for-los alos)
  (cond
    [(empty? alos) ...]
    [else
      (... (first alos) ... (rest alos) ...)]))

Recall, though, that the purpose of a template is to express the data definition as a program layout. That is, a template expresses as code what the data definition for the input expresses as a mix of English and BSL. Hence all important pieces of the data definition must find a counterpart in the template, and this guideline should also hold when a data definition is self-referential. In particular, when a data definition is self-referential in the ith clause and the kth field of the structure mentioned there, the template should be self-referential in the ith cond clause and the selector expression for the kth field. For each such selector expression, add an arrow back to the function parameter. At the end, your template must have as many arrows as we have in the data definition.

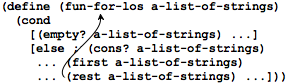Figure 37: Arrows for self-references in templates

Since programming languages are text-oriented, you must learn to use an alternative to arrows, namely, self-applications of the function to the selector expression(s):

(define (fun-for-los alos)
  (cond
    [(empty? alos) ...]
    [else
      (... (first alos) ...
       ... (fun-for-los (rest alos)) ...)]))

We refer to a self-use of a function as recursion and in the context of a template as a natural recursion. The last row in figure 36 addresses the issue of “arrows” in data definitions; some of the following chapters will expand on this idea.

For the design of the body we start with those cond lines that do not contain natural recursions. They are called base cases.The corresponding answers are typically easy to formulate or are already given by the examples.

Then we deal with the self-referential cases. We start by reminding ourselves what each of the expressions in the template line computes. For the natural recursion we assume that the function already works as specified in our purpose statement. The rest is then a matter of combining the various values.

What are the answers for the non-recursive cond clauses?
The examples should tell you which values you need here. If not, formulate appropriate examples and tests.
What do the selector expressions in the recursive clauses compute?
The data definitions tell you what kind of data these expressions extract and the interpretations of the data definitions tell you what this data represents.
What do the natural recursions compute?
Use the purpose statement of the function to determine what the value of the recursion means not how it computes this answer. If the purpose statement doesn't tell you the answer, improve the purpose statement.
How can you combine these values into the desired answer?
If you are stuck here, arrange the examples from the third step in a table. Place the given input in the first column and the desired output in the last column. In the intermediate columns enter the values of the selector expressions and the natural recursion(s). Add examples until you see a pattern emerge that suggests a ``combinator'' function.
Figure 38: How to turn the template into a function definition

Figure 38 formulates questions and answers for this step. Let us use them for the definition of how-many, a function that determines how many strings are on a list of strings. Assuming we have followed the design recipe, we have the following:

; List-of-strings -> Number
; to determine how many strings are on alos
(define (how-many alos)
  (cond
    [(empty? alos) ...]
    [else
     (... (first alos) ... (how-many (rest alos)) ...)]))

The answer for the base case is 0 because the empty list contains nothing. The two expressions in the second clause compute the first item and the number of strings on the (rest alos). To compute how many strings there are on all of alos, we just need to add 1 to the value of the latter expression:

(define (how-many alos)
  (cond
    [(empty? alos) 0]
    [else (+ (how-many (rest alos)) 1)]))

This example illustrates that not all selector expressions in the template are necessarily relevant for the function definition. In contrast, for the motivating example of the preceding section—contains-flatt?—we use both expressions from the template.

In many cases, the combination step can be expressed with BSL’s primitives, for example, +, and, or cons; in some cases, though, you may have to make wishes. See wish lists in Fixed-Size Data. Finally, keep in mind that for some functions, you may need nested conditions.

Last but not least, make sure all the examples are turned into tests, that the tests are run, and that running them covers all the pieces of the function.

Figure 39 summarizes the design recipe of this section in a tabular format. The first column names the steps of the design recipe, the second the expected results of each step. In the third column, we describe the activities that get you there. The figure is tailored to the kind of self-referential list definitions we use in this chapter. As always, practice helps you master the process, so we strongly recommend that you tackle the following exercises, which ask you to apply the recipe to several kinds of examples.

You may want to copy figure 39 onto one side of an index card and write down your favorite versions of the questions and answers in figure 36 and figure 38 onto the back of it. Then carry it with you for future reference. Sooner or later, the design steps become second nature and you won’t think about them anymore. Until then, refer to your index card whenever you are stuck with the design of a function.

steps
outcome
activity
problem analysis
data definition
identify the information that must be represented; develop a data representation; know how to create data for a specific item of information and how to interpret a piece of data as information; identify self-references in the data definition
header
signature; purpose statement; dummy definition
write down a signature, using the names from the data definitions; formulate a concise purpose statement; create a dummy function that produces a constant value from the specified range
examples
examples and tests
work through several examples, at least one per clause in the (self-referential) data definition; turn them into check-expect tests
template
function template
translate the data definition into a template: one cond clauses per clause; one condition per clause to distinguish the cases; selector expressions per clause if the condition identifies a structure; one natural recursion per self-reference in the data definition
definition
full-fledged definition
find a function that combines the values of the expressions in the cond clauses into the expected answer
test
validated tests
run the tests and validate that they all pass
Figure 39: Designing a function for self-referential data

10.1 Finger Exercises: Lists

Exercise 124. Compare the template for how-many and contains-flatt?. Ignoring the function name, they are the same. Explain why.

Exercise 125. Here is a data definition for representing amounts of money:
; A List-of-amounts is one of:
; – empty
; – (cons PositiveNumber List-of-amounts)
; interp. a List-of-amounts represents some amounts of money
Create some examples to make sure you understand the data definition. Also add an arrow for the self-reference.
Design the function sum, which consumes a List-of-amounts and computes the sum of the amounts.

Exercise 126. Now take a look at this data definition:
; A List-of-numbers is one of:
; – empty
; – (cons Number List-of-numbers)
Some elements of this class of data are appropriate inputs for sum from exercise 125 and some aren’t.
Design the function pos?, which consumes a List-of-numbers and determines whether all numbers are positive numbers. In other words, if (pos? l) yields true, then l is an element of List-of-amounts.

Exercise 127. Design the function all-true, which consumes a list of Boolean values and determines whether all of them are true. In other words, if there is any false on the list, the function produces false; otherwise it produces true.
Also design the function one-true, which consumes a list of Boolean values and determines whether at least one item on the list is true.
Follow the design recipe: start with a data definition for lists of Boolean values and don’t forget to make up examples.

Exercise 128. Design the function juxtapose, which consumes a list of strings and appends them all into one long string.

Exercise 129. Design ill-sized?. The function consumes a list of images loi and a positive number n. It produces the first image on loi that is not an n by n square; if it cannot find such an image, it produces false.

10.2 Non-empty Lists

Now you know enough to use cons and to create data definitions for lists. If you solved (some of) the exercises at the end of the preceding section, you can deal with lists of various flavors of numbers, lists of Boolean values, lists of images, and so on. In this section we continue to explore what lists are and how to process them.

Let us start with the simple-looking problem of computing the average of a list of temperatures. To simplify things, we provide the data definitions:

; A List-of-temperatures is one of:
; – empty
; – (cons CTemperature List-of-temperatures)

; A CTemperature is a Number greater or equal to -256.

For our intentions, you should think of temperatures as plain numbers, but the second data definition reminds you that in reality not all numbers are temperatures and you should keep this in mind.

The header material is straightforward:

; List-of-temperatures -> Number
; compute the average temperature
(define (average alot) 0)

Making up examples for this problem is also easy, and so we just formulate one test:

(check-expect (average (cons 1 (cons 2 (cons 3 empty)))) 2)

The expected result is of course the sum of the temperatures divided by the number of temperatures.

A moment’s thought should tell you that the template for average should be similar to the ones we have seen so far:

(define (average alot)
  (cond
    [(empty? alot) ...]
    [(cons? alot)
     (... (first alot) ... (average (rest alot)) ...)]))

The two cond clauses follow from the two clauses of the data definition; the questions distinguish empty lists from non-empty lists; and the natural recursion is needed to compute the average of the rest, which is also a list of numbers.

The problem is that it was too difficult to turn this template into a working function definition. The first cond clause needs a number that represents the average of an empty collection of temperatures, but there is no such number. Even if we ignore this problem for a moment, the second clause demands a function that combines a temperature and an average for many other temperatures into another average. Although it is isn’t impossible to compute this average, it is not the most appropriate way to do so.

When we compute the average of a bunch of temperatures, we divide their sum by the number of temperatures. We said so when we formulated our trivial little example. This sentence, however, suggests that average is a function of three tasks: division, summing, and counting. Our guideline from Fixed-Size Data tells us to write one function per task and if we do so, the design of average is obvious:

; List-of-temperatures -> Number
; compute the average temperature
(define (average alot)
(/ (sum alot)
(how-many alot)))

; List-of-temperatures -> Number
; add up the temperatures on the given list
(define (sum alot) 0)

; List-of-temperatures -> Number
; count the temperatures on the given list
(define (how-many alot) 0)

The last two function definitions are wishes of course for which we need to design complete definitions. Doing so is fortunately easy because how-many from above works for List-of-strings and List-of-temperatures (why?) and because the design of sum follows the same old routine:

; List-of-temperatures -> Number
; add up the temperatures on the given list
(define (sum alot)
  (cond
    [(empty? alot) 0]
    [else (+ (first alot) (sum (rest alot)))]))

Before you read on, turn the example for average into an example for sum and ensure that the test runs properly. Then ensure that the above test for average works out.

When you read this definition of average now, it is obviously correct simply because it directly corresponds to what everyone learns about averaging in school. Still, programs run not just for us but for others. In particular, others should be able to read the signature and use the function and expect an informative answer. But, our definition of average does not work for empty lists of temperatures.

Exercise 130. Determine how average behaves in DrRacket when applied to the empty list of temperatures. Then design checked-average, a function that produces an informative error message when it is applied to empty.

From a theoretical perspective, exercise 130 shows that average is a partial function because it raises an error for empty. The alternative development explains that, in this case, we can narrow down the domain and create a total function. An alternative solution is to inform people through the signature that average doesn’t work for empty lists. To do so, we need a data representation for lists of temperatures that excludes empty, that is, a data definition like this:

; A NEList-of-temperatures is one of:
; – ???
; – (cons CTemperature NEList-of-temperatures)

The questions is with what we should replace “???” so that the empty list is excluded but all other lists of temperatures are still constructable. One hint is that while the empty list is the shortest list, any list of one temperature is the next shortest list. In turn, this suggests that the first clause should describe all possible lists of one temperature:

; A NEList-of-temperatures is one of:
; – (cons CTemperature empty)
; – (cons CTemperature NEList-of-temperatures)
; interp.: non-empty lists of measured temperatures

While this definition differs from the preceding list definitions, it shares the critical elements: a self reference and a clause that does not use a self-reference. Strict adherence to the design recipe demands that you make up some examples of NEList-of-temperatures to ensure that the definition makes sense. As always, you should start with the base clause, meaning the example must look like this:

(cons ccc empty)

where ccc must be replaced by a CTemperature. Given the definition of the latter, here are three one-element lists of temperatures: (cons -256 empty), (cons 3 empty), and (cons 100 empty). Furthermore, it is easy to check that all non-empty elements of List-of-temperatures are also elements of NEList-of-temperatures. For example,

(cons 1 (cons 2 (cons 3 empty))) fits the bill if (cons 2 (cons 3 empty)) does;
and (cons 2 (cons 3 empty)) belongs to NEList-of-temperatures because (cons 3 empty) is an element of NEList-of-temperatures, as confirmed before.

Check for yourself that there is no limit on the size of NEList-of-temperatures.

Let us now return to the problem of designing average so that everyone knows it is for non-empty lists only. With the definition of NEList-of-temperatures we now have the means to say what we want in the signature:

; NEList-of-temperatures -> Number
; compute the average temperature

(check-expect (average (cons 1 (cons 2 (cons 3 empty)))) 2)

(define (average anelot)
(/ (sum anelot)
(how-many anelot)))

Naturally the rest remains the same: the purpose statement, the example-test, and the function definition. After all, the very idea of computing the average assumes a non-empty collection of numbers, and that was the entire point of our discussion.

Exercise 131. Would sum and how-many work for NEList-of-temperatures even if they were designed for inputs from List-of-temperatures? If you think they don’t work, provide counter-examples. If you think they would, explain why.

Nevertheless the definition also raises the question how to design sum and how-many because they consume instances of NEList-of-temperatures now. Here is the obvious result of the first three steps of the design recipe:

; NEList-of-temperatures -> Number
; compute the sum of the given temperatures
(check-expect (sum (cons 1 (cons 2 (cons 3 empty)))) 6)
(define (sum anelot) 0)

The example is adapted from the example for average; the header definition produces a number as requested, but the wrong one for the given test case.

The fourth step is the most interesting part of the design of sum for NEList-of-temperatures. All preceding examples of design demand a template that distinguishes empty lists from non-empty, i.e., consed, lists because the data definitions have an appropriate shape. This is not true for NEList-of-temperatures. Here both clauses add consed lists. The two clauses differ, however, in the rest field of these lists. In particular, the first clause always uses empty in the rest field and the second one uses a consed list instead. Hence the proper questions to distinguish data from the first and the second clause first extract the rest field and then use a predicate:

; NEList-of-temperatures -> Number
(define (sum anelot)
  (cond
    [(empty? (rest anelot)) ...]
    [(cons? (rest anelot)) ...]))

As always, else would be an acceptable replacement for (cons? (rest anelot)) in the second clause, though it would also be less informative.

Next you should inspect both clauses and determine whether one or both of them deal with anelot as if it were a structure. This is of course the case, which the unconditional use of rest on anelot demonstrates. Put differently, you should add appropriate selector expressions to the two clauses:

(define (sum anelot)
  (cond
    [(empty? (rest anelot)) (... (first anelot) ...)]
    [(cons? (rest anelot))
     (... (first anelot) ... (rest anelot) ...)]))

Before you read on, explain why the first clause does not contain the selector expression (rest anelot).

The final question of the template design concerns self-references in the data definition. As you know, NEList-of-temperatures contains one and therefore the template for sum demands one recursive use:

(define (sum anelot)
  (cond
    [(empty? (rest anelot)) (... (first anelot) ...)]
    [(cons? (rest anelot))
     (... (first anelot) ... (sum (rest anelot)) ...)]))

Specifically, sum must be called on (rest anelot) in the second clause because the second clause of the data definition is self-referential at the analogous point.

For the fifth design step, let us understand how much we already have. Since the first cond clause looks significantly simpler than the second one with its recursive function call, you should start with that one. In this particular case, the condition says that sum is applied to a list with exactly one temperature, (first anelot). Clearly, this one temperature is the sum of all temperatures on the given list:

(define (sum anelot)
  (cond
    [(empty? (rest anelot)) (first anelot)]
    [(cons? (rest anelot))
     (... (first anelot) ... (sum (rest anelot)) ...)]))

The second clause says that the list consists of a temperature and at least one more; (first anelot) extracts the first position and (rest anelot) the remaining ones. Furthermore, the template suggests to use the result of (sum (rest anelot)). But sum is the function that you are defining, and you can’t possibly know how it uses (rest anelot). All you do know is what the purpose statement says, namely, that sum adds all the temperatures on the given list, which is (rest anelot). If this statement is true—and this is a leap of faith for now—then (sum (rest anelot)) adds up all but one of the numbers of anelot. To get the total, the function just has to add the first temperature:

(define (sum anelot)
  (cond
    [(empty? (rest anelot)) (first anelot)]
    [(cons? (rest anelot)) (+ (first anelot) (sum (rest anelot)))]))

For the curious among our readers, the design recipe for arbitrarily large data corresponds to so-called “proofs by induction” in mathematics and the “leap of faith” represents the assumption of the induction hypothesis for the inductive step of such a proof. Courses on logic prove the validity of this proof technique with a so-called Induction Theorem. If you now run the example/test for this function, you will see that the leap of faith is justified. Indeed, for reasons beyond this book, this leap of faith is always justified, which is why it is an inherent part of the design recipe.

Exercise 132. Design how-many for NEList-of-temperatures. Ensure that average passes all of its test cases, too.

Exercise 133. Develop a data definition for representing non-empty lists of Boolean values. Then re-design the functions all-true and one-true from exercise 127.

Exercise 134. Compare the function definitions from this section (sum, how-many, all-true, one-true) with the corresponding function definitions from the preceding sections. Is it better to work with data definitions that accommodate empty lists as opposed to definitions for non-empty lists? Why? Why not?

10.3 Natural Numbers

The BSL programming language supplies many functions that consume lists and a few that produce them, too. Among those is make-list, which consumes a number n together with some other value v and produces a list that contains v n times. Here are some examples:

> (make-list 2 "hello")
(cons "hello" (cons "hello" empty))
> (make-list 3 true)
(cons true (cons true (cons true empty)))
> (make-list 0 17)
empty

In short, even though this function consumes atomic data, it produces arbitrarily large pieces of data. Your question should be how this is possible.

Our answer is that make-list’s input isn’t just a number, it is a special kind of number. In kindergarten you called these numbers “counting numbers,” i.e., these numbers are used to count objects. In computer science, these numbers are dubbed natural numbers. Unlike regular numbers, natural numbers come with a data definition:

; A N (Natural Number) is one of:
; – 0
; – (add1 N)

And as you can easily see, this data definition is self-referential just like the data definition for various forms of lists.

Let us take a close look at the data definition of natural numbers. The first clause says that 0 is a natural number; it is of course used to say that there is no object to be counted. The second clause tells you that if n is a natural number, then n+1 is one too, because add1 is a function that adds 1 to whatever number it is given. We could write this second clause as (+ n 1) but the use of add1 is supposed to signal that this addition is special.

What is special about this use of add1 is that it acts more like a constructor from some structure type definition than a regular numeric function. For that reason, BSL also comes with the function sub1, which is the “selector” corresponding to add1. Given any natural number m not equal to 0, you can use sub1 to find out the number that went into the construction of m. Put differently, add1 is like cons and sub1 is like first and rest.

At this point you may wonder what the predicates are that distinguish 0 from those natural numbers that are not 0. There are two, just as for lists: zero?, which determines whether some given number is 0, and positive?, which determines whether some number is larger than 0.

Now you are in a position to design functions such as make-list yourself. The data definition is already available, so let us add the header material:

; N String -> List-of-strings
; create a list of n strings s

(check-expect (copier 2 "hello") (cons "hello" (cons "hello" empty)))
(check-expect (copier 0 "hello") empty)

(define (copier n s)
empty)

Developing the template is the next step. The questions for the template suggest that copier’s body is a cond expression with two clauses: one for 0 and one for positive numbers. Furthermore, 0 is considered atomic and positive numbers are considered structured values, meaning the template needs a selector expression in the second clause. Last but not least, the data definition for N is self-referential in the second clause. Hence the template needs a recursive application to the correspond selector expression in the second clause:

(define (copier n s)
  (cond
    [(zero? n) ...]
    [(positive? n) (... (copier (sub1 n) s) ...)]))

; N String -> List-of-strings
; create a list of n strings s

(check-expect (copier 2 "hello") (cons "hello" (cons "hello" empty)))
(check-expect (copier 0 "hello") empty)

(define (copier n s)
  (cond
    [(zero? n) empty]
    [(positive? n) (cons s (copier (sub1 n) s))]))
Figure 40: Creating a list of copies

Figure 40 contains a complete definition of the copier function, as obtained from its template. Let us reconstruct this step carefully. As always, we start with the cond clause that has no recursive calls. Here the condition tells us that the (important) input is 0 and that means the function must produce a list with 0 items, that is, none. Of course, working through the second example has already clarified this case. Next we turn to the other cond clause and remind ourselves what the expressions from the template compute:

(sub1 n) extracts the natural number that went into the construction of n, which we know is larger than 0;
(copier (sub1 n) s), according to the purpose statement of copier, produces a list of (sub1 n) strings s.

But the function is given n and must therefore produce a list with n strings s. Given a list with one too few strings, it is easy to see that the function must simply cons one s onto the result of (copier (sub1 n) s). And that is precisely what the second clause specifies.

At this point, you should run the tests to ensure that this function works at least for the two worked examples. In addition, you may wish to use the function on some additional inputs.

Exercise 135. Does copier function properly when you apply it to a natural number and a Boolean or an image? Or do you have to design another function? Read Abstraction for an answer.
An alternative definition of copier might use else for the second condition:
(define (copier.v2 n s)
  (cond
    [(zero? n) empty]
    [else (cons s (copier (sub1 n) s))]))
How do copier and copier.v2 behave when you apply them to 10.1 and "xyz"? Explain.

Exercise 136. Design the function add-to-pi. It consumes a natural number n and adds it to pi without using + from BSL. Here is a start:
; N -> Number
; compute (+ n pi) without using +

(check-within (add-to-pi 3) (+ 3 pi) 0.001)

(define (add-to-pi n)
pi)
Once you have a complete definition, generalize the function to add, which adds a natural number n to some arbitrary number x without using +. Why does the skeleton use check-within?

Exercise 137. Design the function multiply. It consumes a natural number n and multiplies it with some arbitrary number x without using *.

Exercise 138. Design two functions: col and row.
The function col consumes a natural number n and an image i. It produces a column—a vertical arrangement—of n copies of i.
The function row consumes a natural number n and an image i. It produces a row—a horizontal arrangement—of n copies of i
Use the two functions to create a rectangle of 8 by 18 squares, each of which has size 10 by 10.

Exercise 139. Design a program that visualizes a 1968-style European student riot. A small group of students meets to make paint-filled balloons, enters some lecture hall and randomly throws the balloons at the attendees.
The program’s only input should be a natural number, which represents the number of balloons. The program should produce an image that contains a black grid, which represents the seats, and the positions of the balls:
You may wish to re-use the functions from exercise 138.

10.4 Russian Dolls

Wikipedia defines a Russian doll as “ a set of dolls of decreasing sizes placed one inside the other.” The paragraph is accompanied by an appropriate picture of dolls:

Of course, here the dolls are taken apart so that the viewer can see them all.

The problem may strike you as somewhat abstract or even absurd; after all it isn’t clear why you would want to represent Russian dolls or what you would do with such a representation. Suspend your disbelief and read along; it is a worthwhile exercise. Now consider the problem of representing such Russian dolls with BSL data. With a little bit of imagination, it is easy to see that an artist can create a nest of Russian dolls that consists of an arbitrary number of dolls. After all, it is always possible to wrap another layer around some given Russian doll. Then again, you also know that deep inside there is a solid doll without anything inside.

For each layer of a Russian doll, we could care about many different things: its size, though it is related to the nesting level; its color; the image that is painted on the surface; and so on. Here we just pick one, namely the color of the doll, which we represent with a string. Given that, we know that each layer of the Russian doll has two properties: its color and the doll that is inside. To represent pieces of information with two properties, we always define a structure type:

(define-struct layer (color doll))

And then we add a data definition:

; An RD (russian doll) is one of:
; – String
; – (make-layer String RD)

Naturally, the first clause of this data definition represents the innermost doll or, to be precise, its color. The second clause is for adding a layer around some given Russian doll. We represent this with an instance of layer, which obviously contains the color of the doll and one other field: the doll that is nested immediately inside of this doll.

Take a look at this doll:

It consists of three dolls. The red one is the innermost one, the green one sits in the middle, and the yellow is the current outermost wrapper. To represent this doll with an element of RD, you start on either end. We proceed from the inside out. The red doll is easy to represent as an RD. Since nothing is inside and since it is red, the string "red" will do fine. For the second layer, we use

(make-layer "green" "red")

which says that a green (hollow) doll contains a the red doll. Finally, to get the outside we just wrap another layer around this last doll:

(make-layer "yellow" (make-layer "green" "red"))

This process should give you a good idea how to go from any set of colored Russian dolls to a data representation. But keep in mind that a programmer must also be able to do the converse, that is, go from a piece of data to concrete information. In this spirit, draw a schematic Russian doll for the following element of RD:

(make-layer "pink" (make-layer "black" "white"))

You might even try this in BSL.

Now that we have a data definition and understand how to represent actual dolls and how to interpret elements of RD as dolls, we are ready to design functions that consume RDs. Specifically, let us design the function that counts how many dolls a Russian doll set contains. This sentence is a fine purpose statement and determines the signature, too:

; RD -> Number
; how many dolls are part of an-rd

As for examples, let us start with (make-layer "yellow" (make-layer "green" "red")). The image above tells us that 3 is the expected answer because there are three dolls: the red one, the green one, and the yellow one. Just working through this one example, also tells us that when the input is a representation of this doll

then the answer is 1.

Step four demands the development of a template. Using the standard questions for this step produces this template:

; RD -> Number
; how many dolls are a part of an-rd
(define (depth an-rd)
  (cond
    [(string? an-rd) ...]
    [(layer? an-rd)
     (... (layer-color an-rd) ... (depth (layer-doll an-rd)) ...)]))

The number of cond clauses is determined by the number of clauses in the definition of RD. Each of the clauses specifically spells out what kind of data it is about, and that tells us which predicates to use: string? and layer?. While strings aren’t compound data, instances of layer contain two values. If the function needs these values, it uses the selector expressions (layer-color an-rd) and (layer-doll an-rd). Finally, the second clause of the data definition contains a self-reference from the doll field of the layer structure to the definition itself. Hence we need a recursive function call for the second selector expression.

The examples and the template almost dictate the function definition. For the non-recursive cond clause, the answer is obviously 1. For the recursive clause, the template expressions compute the following results:

(layer-color an-rd) extracts the string that describes the color of the current layer;
(layer-doll an-rd) extracts the doll contained within the current layer; and
according to the purpose statement, (depth (layer-doll an-rd)) determines how many dolls (layer-doll an-rd) consists of.

This last number is almost the desired answer but not quite because the difference between an-rd and (layer-doll an-rd) is one layer meaning one extra doll. Put differently, the function must add 1 to the recursive result to obtain the actual answer:

; RD -> Number
; how many dolls are a part of an-rd
(define (depth an-rd)
  (cond
    [(string? an-rd) 1]
    [(layer? an-rd) (+ (depth (layer-doll an-rd)) 1)]))

Note how the function definition does not use (layer-color an-rd) in the second clause. Once again, we see that the template is an organization schema for everything we know about the data definition but we may not need all of these pieces for the actual definition.

Last but not least, we must translate the examples into tests:

(check-expect (depth (make-layer "yellow" (make-layer "green" "red")))
3)
(check-expect (depth "red")
1)

If you run these in DrRacket, you will see that their evaluation touches all pieces of the definition of depth.

Exercise 140. Design the function colors. It consumes a Russian doll and produces a string of all colors, separate by a comma and a space. Thus our example should produce
"yellow, green, red"

Exercise 141. Design the function inner, which consumes an RD and produces the (color of the) innermost doll.

10.5 Lists And World

With lists and self-referential data definitions in general, you can design and run many more interesting world programs than with finite data. Just imagine you can now create a version of the space invader program from Itemizations and Structures that allows the player to fire as many shots from the tank as desired. Let us start with a simplistic version of this problem:

Sample Problem: Design a world program that simulates firing shots. Every time the “player” hits the space bar, the program adds a shot to the bottom of the canvas. These shots rise vertically at the rate of one pixel per tick.

If you haven’t designed a world program in a while, re-read section Designing World Programs.

Designing a world program starts with a separation of information into constants and elements of the ever-changing state of the world. For the former we introduce physical and graphical constants; for the latter we need to develop a data representation for world states. While the sample problem is relatively vague about the specifics, it clearly assumes a rectangular scenery with shots painted along a vertical line. Obviously the locations of the shots change with every clock tick but the size of the scenery and x coordinate of the line of shots remain the same:

; physical constants
(define HEIGHT 80)
(define WIDTH 100)
(define XSHOTS (/ WIDTH 2))

; graphical constants
(define BACKGROUND (empty-scene WIDTH HEIGHT))
(define SHOT (triangle 3 "solid" "red"))

Nothing in the problem statement demands these particular choices, but as long as they are easy to change—meaning changing by editing a single definition—we have achieved our goal.

As for those aspects of the “world” that change, the problem statement mentions two. First, hitting the space bar adds a shot. Second, all the shots move straight up by one pixel per clock tick. Given that we cannot predict how many shots the player will “fire,” we use a list to represent them:

; A List-of-shots is one of:
; – empty
; – (cons Shot List-of-shots)
; interp.: the collection of shots fired and moving straight up

The one remaining question is how to represent each individual shot. We already know that all of them have the same x coordinate and that this coordinate stays the same throughout. Furthermore, all shots look alike. Hence, their y coordinates are the only property in which they differ from each other. It therefore suffices to represent each shot as a number:

; A Shot is a Number.
; interp.: the number represents the shot's y coordinate

We could restrict the representation of shots to the interval of numbers below HEIGHT because we know that all shots are launched from the bottom of the canvas and that they then move up, meaning their y coordinate continuously decreases.

Of course, you can also use a data definition like this to represent this world:

; A ShotWorld is List-of-numbers.
; interp.: each number represents the y coordinate of a shot

After all, the above two definitions describe all list of numbers; we already have a definition for lists of numbers; and the name ShotWorld tells everyone what this class of data is about.

Once you have defined constants and developed a data representation for the states of the world, the key task is to pick which event handlers you wish to employ and to adapt their signatures to the given problem. The running example mentions clock ticks and the space bar, all of which translates into a wish list of three functions:

the function that turns a world state into an image:
; ShotWorld -> Image
; add each shot y on w at (MID,y) to the background image
(define (to-image w)
BACKGROUND)
because the problem demands a visual rendering;
one for dealing with tick events:
; ShotWorld -> ShotWorld
; move each shot up by one pixel
(define (tock w)
w)
and one function for dealing with key events:
; ShotWorld KeyEvent -> ShotWorld
; add a shot to the world if the space bar was hit
(define (keyh w ke)
w)

Don’t forget that in addition to the initial wish list, you also need to define a main function that actually sets up the world and installs the handlers. Figure 41 includes this one function that is not designed but defined as a modification of standard schema.

Let us start with the design of to-image. We have its signature, purpose statement and header, so we need examples next. Since the data definition has two clauses, there should be at least two examples: empty and a consed list, say, (cons 10 empty). The expected result for empty is obviously BACKGROUND; if there is a y coordinate, though, the function must place the image of a shot at MID and the specified coordinate:

(check-expect (to-image (cons 10 empty))
(place-image SHOT XSHOTS 10 BACKGROUND))

Before you read on, work through an example that applies to-image to a list of two shot representations. It helps to do so to understand how the function works.

The fourth step of the design is to translate the data definition into a template:

; ShotWorld -> Image
(define (to-image w)
  (cond
    [(empty? w) ...]
    [else ... (first w) ... (to-image (rest w)) ...]))

The template for data definitions for lists is so familiar now that it doesn’t need much explanation. If you have any doubts, read over the questions in figure 36 and design the template on your own.

From here it is straightforward to define the function. The key is to combine the examples with the template and to answer the questions from figure 38. Following those, you start with the base case of an empty list of shots and, from the examples, you know that the expected answer is BACKGROUND. Next you formulate what the template expressions in the second cond compute:

(first w) extracts the first coordinate from the list;
(rest w) is the rest of the coordinates; and
according to the purpose statement of the function, (to-image (rest w)) adds each shot on (rest w) to the background image.

In other words, (to-image (rest w)) renders the rest of the list as an image and thus does almost all the work. What is missing from this image is the first shot, (first w). If you now apply the purpose statement to these two expressions, you get the desired expression for the second cond clause:

(place-image SHOT XSHOTS (first w) (to-image (rest w)))

The added icon is the standard image for a shot; the two coordinates are spelled out in the purpose statement; and the last argument to place-image is the image constructed from the rest of the list.

; physical constants
(define HEIGHT 80)
(define WIDTH 100)
(define XSHOTS (/ WIDTH 2))

; graphical constants
(define BACKGROUND (empty-scene WIDTH HEIGHT))
(define SHOT (triangle 3 "solid" "red"))

; A ShotWorld is List-of-numbers.
; interp.: the collection of shots fired and moving straight up

; ShotWorld -> ShotWorld
; move each shot up by one pixel
(define (tock w)
  (cond
    [(empty? w) empty]
    [else (cons (sub1 (first w)) (tock (rest w)))]))

; ShotWorld KeyEvent -> ShotWorld
; add a shot to the world if the space bar was hit
(define (keyh w ke)
  (cond
    [(key=? ke " ") (cons HEIGHT w)]
    [else w]))

; ShotWorld -> Image
; add each shot y on w at (MID,y) to the background image
(define (to-image w)
  (cond
    [(empty? w) BACKGROUND]
    [else (place-image SHOT XSHOTS (first w) (to-image (rest w)))]))

; ShotWorld -> ShotWorld
(define (main w0)
  (big-bang w0
            (on-tick tock)
            (on-key keyh)
            (to-draw to-image)))
Figure 41: A list-based world program

Figure 41 displays the complete function definition for to-image and indeed the rest of the program, too. The design of tock is just like the design of to-image and you should work through it for yourself. The signature of the keyh handler, though, poses one interesting question. It specifies that the handler consumes two inputs with non-trivial data definitions. On one hand, the ShotWorld is self-referential data definition. On the other hand, the definition for KeyEvents is a large enumeration. For now, we have you “guess” which of the two arguments should drive the development of the template; later we will study such cases in depth.

As far as a world program is concerned, a key handler such as keyh is about the key event that it consumes. Hence, we consider it the main argument and use its outline to derive the template. Specifically, following the data definition for KeyEvent from Enumerations it dictates that the function needs a cond expression with numerous clauses like this:

(define (keyh w ke)
  (cond
    [(key=? ke "left") ...]
    [(key=? ke "right") ...]
    ...
    [(key=? ke " ") ...]
    ...
    [(key=? ke "a") ...]
    ...
    [(key=? ke "z") ...]))

Of course, just like for functions that consume all possible BSL values, a key handler usually does not need to inspect all possible cases. For our running problem, you specifically know that the key handler reacts only to the space bar and all others are ignored. So it is natural to collapse all of the cond clauses into an else clause except for the clause for " ".

Exercise 142. Equip the program in figure 41 with tests and make sure it passes those. Explain what main does. Then run the program via main.

Exercise 143. Experiment whether the arbitrary decisions concerning constants are truly easy to change. For example, determine whether changing a single constant definition achieves the desired outcome:
change the height of the canvas to 220 pixels;
change the width of the canvas to 30 pixels;
change the x location of the line of shots to “somewhere to the left of the middle;”
change the background to a green rectangle; and
change the rendering of shots to a red elongated rectangle.
Also check whether it is possible to double the size of the shot without changing anything else, change its color to black, or change its form to "outline".

Exercise 144. If you run main, press the space bar (fire a shot), and wait for a good amount of time, the shot disappears from the canvas. When you shut down the world canvas, however, the result is a world that still contains this invisible shot.
Design an alternative tock function, which not just moves shots one pixel per clock tick but also eliminates those whose coordinates places them above the canvas. Hint: You may wish to consider the design of an auxiliary function for the recursive cond clause.

Exercise 145. Turn the exercise of exercise 139 into a world program. Its main function should consume the rate at which to display the balloon throwing:
; Number -> ShotWorld
; display the student riot at rate ticks per second
(define (main rate)
  (big-bang empty
            (on-tick drop-balloon rate)
            (stop-when long-enough)
            (to-draw to-image)))
Naturally, the riot should stop when the students are out of balloons.

11 More on Lists

11.1 Functions that Produce Lists

Here is a function for determining the wage of an hourly employee:

; Number -> Number
; compute the wage for h hours of work
(define (wage h)
(* 12 h))

It consumes the number of hours worked and produces the wage. A company that wishes to use payroll software isn’t interested in this function, however. It wants a function that computes the wages for all of its employees.

Call this new function wage*. Its task is to process all employee work hours and to determine the wages due to each of them. For simplicity, let us assume that the input is a list of numbers, each representing the number of hours that one employee worked, and that the expected result is a list of the weekly wages earned, also represented with a list of numbers.

Since we already have a data definition for the inputs and outputs, we can immediately move to the second design step:

; List-of-numbers -> List-of-numbers
; compute the weekly wages for all given weekly hours
(define (wage* alon)
empty)

Next you need some examples of inputs and the corresponding outputs. So you make up some short lists of numbers that represent weekly work hours:

given:	expected:
empty	empty
(cons 28 empty)	(cons 336 empty)
(cons 40 (cons 28 empty))	(cons 480 (cons 336 empty))

In order to compute the output, you determine the weekly wage for each number on the given input list. For the first example, there are no numbers on the input list so the output is empty. Make sure you understand why the second and third expected output is what you want.

Given that wage* consumes the same kind of data as several other functions from Lists and given that a template depends only on the shape of the data definition, you can reuse these template:

(define (wage* alon)
  (cond
    [(empty? alon) ...]
    [else (... (first alon) ... (wage* (rest alon)) ...)]))

In case you want to practice the development of templates, use the questions from figure 36.

It is now time for the most creative design step. Following the design recipe, we consider each cond-line of the template in isolation. For the non-recursive case, (empty? alon) is true, meaning the input is empty. The examples from above specify the desired answer, empty, and so we are done.

In the second case, the design questions tell us to state what each expression of the template computes:

(first alon) yields the first number on alon, which is the first number of hours worked;
(rest alon) is the rest of the given list; and
(wage* (rest alon)) says that the rest is processed by the very function we are defining. As always we use its signature and its purpose statement to figure out the result of this expression. The signature tell us that it is a list of numbers, and the purpose statement explains that this list represents the list of wages for its input, which is the rest of the list of hours.

The key is to rely on these facts when you formulate the expression that computes the result in this case—even though the function is not yet defined.

Since we already have the list of wages for all but the first item of alon, the function must perform two computations to produce the expected output for the entire alon: compute the weekly wage for (first alon) and construct the list that represents all weekly wages for alon from the first weekly wage and the result of the recursion. For the first part, we reuse wage. For the second, we cons the two pieces of information together into one list:

(cons (wage (first alon)) (wage* (rest alon)))

And with that, the definition is complete: see figure 42.

; List-of-numbers -> List-of-numbers
; compute the weekly wages for all given weekly hours
(define (wage* alon)
  (cond
    [(empty? alon) empty]
    [else (cons (wage (first alon)) (wage* (rest alon)))]))

; Number -> Number
; compute the wage for h hours of work
(define (wage h)
  (* 12 h))
Figure 42: Computing the wages of all employees

Exercise 146. Translate the examples into tests and make sure they all succeed. Then change the function in figure 42 so that everyone gets $14 per hour. Now revise the entire program so that changing the wage for everyone is a single change to the entire program and not several.

Exercise 147. No employee could possibly work more than 100 hours per week. To protect the company against fraud, the function should check that no item of the input list of wage* exceeds 100. If one of them does, the function should immediately signal an error. How do we have to change the function in figure 42 if we want to perform this basic reality check?

Show the products of the various steps in the design recipe. If you are stuck, show someone how far you got according to the design recipe. The recipe isn’t just a design tool for you to use; it is also a diagnosis system so that others can help you help yourself.

Exercise 148. Design convertFC. The function converts a list of Fahrenheit measurements to a list of Celsius measurements.

Exercise 149. Design the function convert-euro, which converts a list of U.S. dollar amounts into a list of euro amounts. Look up the current exchange rate in a newspaper.
Generalize convert-euro to the function convert-euro*, which consumes an exchange rate and a list of dollar amounts and converts the latter into a list of euro amounts.

Exercise 150. Design the function subst-robot, which consumes a list of toy descriptions (strings) and replaces all occurrences of "robot" with "r2d2"; all description remain the same.
Generalize subst-robot to the function substitute. The new function consumes two strings, called new and old, and a list of strings. It produces a new list of strings by substituting all occurrences of old with new.

11.2 Structures In Lists

Representing a work week as a number is a bad choice because the printing of a paycheck requires more information than hours worked per week. Also, not all employees earn the same amount per hour. Fortunately a list may contain items other than atomic values; indeed, lists may contain whatever values we want, especially structures.

Our running example calls for just such a data representation. Instead of numbers, we use structures that contain information about the employee, including the work hours:

(define-struct work (employee rate hours))
; Work is a structure: (make-work String Number Number).
; interp. (make-work n r h) combines the name (n)
; with the pay rate (r) and the number of hours (h) worked.

While this representation is still simplistic, it poses just enough of an additional challenge because it forces us to formulate a data definition for lists that contain structures:

; Low (list of works) is one of:
; – empty
; – (cons Work Low)
; interp. an instance of Low represents the work efforts
; of some hourly employees

Here are three elements of Low:

empty
(cons (make-work "Robby" 11.95 39)
      empty)
(cons (make-work "Matthew" 12.95 45)
      (cons (make-work "Robby" 11.95 39)
            empty))

Use the data definition to explain why these pieces of data belong to Low.

Now that you know that the definition of Low makes sense, it is time to re-design the function wage* so that it consumes elements of Low not just lists of numbers:

; Low -> List-of-numbers
; compute the weekly wages for all given weekly work records
(define (wage*.v2 an-low)
empty)

When you work on real-world projects, you won’t use such suffixes; instead you will use a mechanism for managing different versions of the same code. The suffix “.v2” at the end of the function name informs every reader of the code that this is a second, revised version of the function. In this case, the revision starts with a new signature and an adapted purpose statement. The header is the same as above.

The third step of the design recipe is to work through an example. Let us start with the second list above. It contains one work record, namely, (make-work "Robby" 11.95 39). Its interpretation is that "Robby" worked for 39 hours and that he is paid at the rate of $11.95 per hour. Hence his wage for the week is $466.05, i.e., (* 11.95 39). The desired result for wage*.v2 is therefore (cons 466.05 empty). Naturally, if the input list contained two work records, we would perform this kind of computation twice, and the result would be a list of two numbers. Before you read on, determine the expected result for the third data example above.

Note: Keep in mind that BSL—unlike most other programming languages—understands decimal numbers just like you do, namely, as exact fractions. A language like Java, for example, would produce 466.04999999999995 for the expected wage of the first work record. Since you cannot predict when operations on decimal numbers behave in this strange way, you are better off writing down such examples as

(check-expect
(wage*.v2 (cons (make-work "Robby" 11.95 39) empty))
(cons (* 11.95 39) empty))

just to prepare yourself for other languages. Then again, writing down the example in this style also means you have really figured out how to compute the wage. End of Note

From here we move on to the development of the template. If you use the template questions, you quickly get this much:

(define (wage*.v2 an-low)
  (cond
    [(empty? an-low) ...]
    [(cons? an-low)
     (... (first an-low) ... (wage*.v2 (rest an-low)) ...)]))

because the data definition consists of two clauses, because it introduces empty in the first clause and consed structures in the second, and so on. But, you also realize that you know even more about the input than this template expresses. For example, you know that (first an-low) extracts a structure of three fields from the given list. This seems to suggest the addition of three more expressions to the template:

(define (wage*.v2 an-low)
  (cond
    [(empty? an-low) ...]
    [(cons? an-low)
     (... (first an-low) ... (work-employee (first an-low)) ...
      (work-rate (first an-low)) ... (work-hours (first an-low))
      (wage*.v2 (rest an-low)) ...)]))

This way you would remember that the structure contains potentially interesting data.

We use a different strategy, however. Specifically, we suggest to create and to refer to a separate function template whenever you are developing a template for a data definition that refers to another data definitions:

(define (wage*.v2 an-low)
  (cond
    [(empty? an-low) ...]
    [(cons? an-low)
     (... (for-work (first an-low))
      ... (wage*.v2 (rest an-low)) ...)]))

; Work -> ???
; a template for functions that process work structures
(define (for-work w)
  (... (work-employee w) ... (work-rate w)
   ... (work-hours w) ...))

Splitting the templates leads to a natural partition of work into functions and among functions; none of them grow too large, and all of them relate to a specific data definition.

Finally, you are ready to program. As always you start with the simple-looking case, which is the first cond line here. If wage*.v2 is applied to empty, you expect empty back and that settles it. Next you move on to the second line and remind yourself of what these expressions compute:

(first an-low) extracts the first work structure from the list;
(for-work ...) says that you wish to design a function that processes work structures;
(rest an-low) extracts the rest of the given list; and
according to the purpose statement, (wage*.v2 (rest an-low)) determines the list of wages for all the work records other than the first one.

If you are stuck here, use the examples to illustrate what these reminders mean.

If you understand it all, you see that it is enough to cons the two expressions together:

... (cons (for-work (first an-low))
(wage*.v2 (rest an-low))) ...

assuming that for-work computes the wage for the first work record. In short, you have finished the function by adding another entry to your wish list of functions.

Since for-work is a name that just serves as a stand-in and since it is a bad name for this function, let us call the function wage.v2 and write down its complete wish list entry:

; Work -> Number
; compute the wage for the given work record w
(define (wage.v2 w)
0)

This design of this kind of function is extensively covered in Fixed-Size Data and thus doesn’t need any additional explanation here. Figure 43 shows the final result of developing wage and wage*.v2.

; Low -> List-of-numbers
; compute the weekly wages for all given weekly work records

(check-expect (wage*.v2 (cons (make-work "Robby" 11.95 39) empty))
              (cons (* 11.95 39) empty))

(define (wage*.v2 an-low)
  (cond
    [(empty? an-low) empty]
    [(cons? an-low) (cons (wage.v2 (first an-low))
                          (wage*.v2 (rest an-low)))]))

; Work -> Number
; compute the wage for the given work record w
(define (wage.v2 w)
  (* (work-rate w) (work-hours w)))
Figure 43: Computing the wages from work records

Exercise 151. The wage*.v2 function consumes a list of work records and produces a list of numbers. Of course, functions may also produce lists of structures.
Develop a data representation for pay checks. Assume that a pay check contains two pieces of information: the name of the employee and an amount. Then design the function wage*.v3. It consumes a list of work records and computes a list of (representations of) pay checks from it, one per work record.
In reality, a pay check also contains an employee number. Develop a data representation for employee information and change the data definition for work records so that it uses employee information and not just a string for the employee’s name. Also change your data representation of pay checks so that it contains an employee’s name and number, too. Finally, design wage*.v4, a function that maps lists of revised work records to lists of revised pay checks.
Note: This exercise demonstrates the iterative refinement of a task. Instead of using data representations that include all relevant information, we started from simplistic representation of pay checks and gradually made the representation realistic. For this simple program, refinement is overkill; later we will encounter situations where iterative refinement is not just an option but a necessity.

Exercise 152. Design the function sum, which consumes a list of Posns and produces the sum of all of its x coordinates.

Exercise 153. Design the function translate. It consumes and produces lists of Posns. For each Posn (x,y) in the former, the latter contains (x,y+1).—We borrow the word “translate” from geometry, where the movement of a point by a constant distance along a straight line is called a translation.

Exercise 154. Design the function legal. Like translate from exercise 153 the function consumes and produces a list of Posns. The result contains all those Posns whose x coordinates are between 0 and 100 and whose y coordinates are between 0 and 200.

Exercise 155. Here is one way to represent a phone number:
(define-struct phone (area switch four))
; A Phone is a structure:
; (make-phone Three Three Four)
; A Three is between 100 and 999.
; A Four is between 1000 and 9999.
Design the function replace. It consumes a list of Phones and produces one. It replaces all occurrence of area code 713 with 281.

11.3 Lists In Lists, Files

Functions And Programs introduces read-file, a function for reading an entire text file as a string. In other words, the creator of read-file chose to represent text files as strings, and the function creates the data representation for specific files (specified by a name). Text files aren’t plain long texts or strings, however. They are organized into lines and words, rows and cells, and many other ways. In short, representing the content of a file as a plain string might work on rare occasions but is usually a bad choice.

For concreteness, take a look at this sample files, dubbed "ttt.txt":

ttt.txt
TTT

Put up in a place
where it's easy to see
the cryptic admonishment
T.T.T.

When you feel how depressingly
slowly you climb,
it's well to remember that
Things Take Time.

Piet Hein

It contains a poem by Piet Hein, and it consists of many lines and words. When you use the program

(require 2htdp/batch-io)
(read-file "ttt.txt")

to turn this file into a BSL string, you get this:

"TTT\n \nPut up in a place\nwhere ..."

where the "\n" inside the string indicates line breaks. (The “...” aren’t really a part of the result as you probably guessed.)

While it is indeed possible to break apart this string with primitive operations on strings, e.g., explode, most programming languages—including BSL—support many different representations of files and functions that create such representations from existing files:

One way to represent this file is as a list of lines, where each line is represented as one string:
(cons "TTT"
  (cons ""
    (cons "Put up in a place"
      (cons ...
        empty))))
Here the second item of the list is the empty string because the file contains an empty line.
Another way is to use a list of all possible words, again each word represented to a string:
(cons "TTT"
  (cons "Put"
    (cons "up"
      (cons "in"
        (cons ...
          empty)))))
Note how the empty second line disappears with this representation. After all, there are no words on the empty line.
And a third representation mixes the first two with a list of list of words:
(cons (cons "TTT" empty)
  (cons empty
    (cons (cons "Put" (cons "up" (cons "in" (cons ... empty))))
      (cons ...
        empty))))
The advantage of this representation over the second one is that it preserves the organization of the file, including the emptiness of the second line. Of course, the price is that all of a sudden lists contain lists.

While the idea of list-containing lists may sound frightening at first, you shouldn’t worry. The design recipe helps even with such complicated forms of data.

Before we get started, take a look at figure 44. It introduces a number of useful file reading functions that come with BSL. They are not comprehensive and there are many other ways of dealing with text from files, and you will need to know a lot more to deal with all possible text files. For our purposes here—teaching and learning the principles of systematic program design—they suffice, and they empower you to design reasonably interesting programs.

; String -> String
; produces the content of file f as a string
(define (read-file f) ...)

; String -> List-of-string
; produces the content of file f as a list of strings,
; one per line
(define (read-lines f) ...)

; String -> List-of-string
; produces the content of file f as a list of strings,
; one per word
(define (read-words f) ...)

; String -> List-of-list-of-string
; produces the content of file f as a list of list of
; strings, one list per line and one string per word
(define (read-words/line f) ...)

; All functions that read a file consume the name of a file
; as a String argument. They assume the specified file
; exists in the same folder as the program; if not they
; signal an error.
Figure 44: Reading files

One problem with figure 44 is that they use the names of two data definitions that do not exist yet, including one involving list-containing lists. As always, we start with a data definition, but this time, we leave this task to you. Hence, before you read on, solve the following exercises. The solutions are needed to make complete sense out of the figure, and without working through the solutions, you cannot really understand the rest of this section.

Exercise 156. You know what the data definition for List-of-strings looks like. Spell it out. Make sure that you can represent Piet Hein’s poem as an instance of the definition where each line is a represented as a string and another one where each word is a string. Use read-lines and read-words to confirm your representation choices.
Next develop the data definition for List-of-list-of-strings. Again, represent Piet Hein’s poem as an instance of the definition where each line is a represented as a list of strings, one per word, and the entire poem is a list of such line representations. You may use read-words/line to confirm your choice.

As you probably know, operating systems come with programs that measure various statistics of files. Some count the number of lines, others count the number of words in a file. A third may determine how many words appear per line. Let us start with the latter to illustrate how the design recipe helps with the design of complex functions.

The first step is to ensure that we have all the necessary data definitions. If you solved the above exercise, you have a data definition for all possible inputs of the desired function, and the preceding section defines List-of-numbers, which describes all possible inputs. To keep things short, we use LLS to refer to the class of lists of lists of strings, and use it to write down the header material for the desired function:

; LLS -> List-of-numbers
; determine the number of words on each line

(define (words-on-line lls)
empty)

We name the functions words-on-line, because it is appropriate and captures the purpose statement in one phrase.

What is really needed though is a set of examples. Here are some data examples:

(define line0 (cons "hello" (cons "world" empty)))
(define line1 empty)

(define lls0 empty)
(define lls1 (cons line0 (cons line1 empty)))

The first two definitions introduce two examples of lines: one contains two words, the other contains none. The last two definitions show how to construct instances of LLS from these line examples. Determine what the expected result is when the function is given these two examples.

Once you have data examples, it is easy to formulate functional examples; just imagine applying the function to each of the data example. When apply words-on-line to lls0, you should get the empty list back, because there are no lines. When you apply words-on-line to lls1, you should get a list of two numbers back, because there are two lines. The two numbers are 2 and 0, respectively, given that the two lines in lls1 contain two and no words each.

Here is how you translate all this into test cases:

(check-expect (words-on-line lls0) empty)
(check-expect (words-on-line lls1) (cons 2 (cons 0 empty)))

You can do this at the end of the second step or for the last step. Doing it now, means you have a complete program, though running it just fails some of the test cases.

The development of the template is the interesting step for this sample problem. By answering the template questions from figure 36, you get the usual list-processing template immediately:

(define (words-on-line lls)
  (cond
    [(empty? lls) ...]
    [else
     (... (first lls) ; a list of strings
      ... (words-on-line (rest lls)) ...)]))

As in the preceding subsection, we know that the expression (first lls) extracts a List-of-strings, which has a complex organization, too. The temptation is to insert a nested template to express this knowledge, but as you should recall, the better idea is to develop a second auxiliary template and to change the first line in the second condition so that it refers to this auxiliary template.

Since this auxiliary template is for a function that consumes a list, the template looks nearly identical to the previous one:

(define (line-processor ln)
  (cond
    [(empty? lls) ...]
    [else
     (... (first ln) ; a string
      ... (line-processor (rest ln)) ...)]))

The important differences are that (first ln) extracts a string from the list and that we consider strings as atomic values. With this template in hand, we can change the first line of the second case in words-on-line to

... (line-processor (first lls)) ...

which reminds us for the fifth step that the definition for words-on-line may demand the design of an auxiliary function.

Now it is time to program. As always, we use the questions from figure 38 to guide this step. The first case, concerning empty lists of lines, is the easy case. Our examples tell us that the answer in this case is empty, i.e., the empty list of numbers. The second, concerning constructed lists, case contains several expressions and we start with a reminder of what they compute:

(first lls) extracts the first line from the non-empty list of (represented) lines;
(line-processor (first lls)) suggests that we may wish to design an auxiliary function to process this line;
(rest lls) is the rest of the list of line;
(words-on-line (rest lls)) computes a list of words per line for the rest of the list. How do we know this? We promised just that with the signature and the purpose statement for words-on-line.

Assuming we can design an auxiliary function that consumes a line and counts the words on one line—let us call this function words#—it is easy to complete the second condition:

(cons (words# (first lls)) (words-on-line (rest lls)))

This expressions conses the number of words on the first line of lls onto a list of numbers that represents the number of words on the remainder of lines of lls.

It remains to design the words# function. Its template is dubbed line-processor and its purpose is to count the number of words on a line, which is just a list of strings. So here is the wish-list entry:

; List-of-strings -> Number
; count the number of words on los
(define (words# los) 0)

At this point, you may recall the example used to illustrate the design recipe for self-referential data in Designing With Self-Referential Data Definitions. The function is called how-many, and it too counts the number of strings on a list of strings. Even though the inputs for how-many is supposed to represent a list of names, this difference simply doesn’t matter; as long as it correctly counts the number of strings on a list of strings, how-many solves our problem.

Since it is always good to reuse existing solutions, one way to define words# is

(define (words# los)
(how-many los))

In reality, however, programming languages come with functions that solve such problems already. BSL calls this function length, and it counts the number of values on any list of values, no matter what the values are.

; A LLS is one of:
; – empty
; – (cons Los LLS)
; interp. a list of lines, each line is a list of strings

(define line0 (cons "hello" (cons "world" empty)))
(define line1 empty)

(define lls0 empty)
(define lls1 (cons line0 (cons line1 empty)))

; LLS -> List-of-numbers
; determine the number of words on each line

(check-expect (words-on-line lls0) empty)
(check-expect (words-on-line lls1) (cons 2 (cons 0 empty)))

(define (words-on-line lls)
  (cond
    [(empty? lls) empty]
    [else (cons (length (first lls))
                (words-on-line (rest lls)))]))
Figure 45: Counting the words on a line

You may wish to look over the rest of functions that come with BSL. Some may look obscure now, but they may just be useful in one of the upcoming problems. Then again, using such functions saves only your time. You just may wish to design them from scratch to practice your design skills or to fill time.

Figure 45 summarizes the full design for our sample problem. The figure includes two test cases. Also, instead of using the separate function words#, the definition of words-on-line simply calls the length function that comes with BSL. Experiment with the definition in DrRacket and make sure that the two test cases cover the entire function definition.

With one small step, you can now design your first file utility:

; String -> List-of-numbers
; count the number of words on each line in the given file
(define (file-statistic file-name)
(words-on-line
(read-words/line file-name)))

The function composes the library function with the just designed words-on-line function. The former reads a file as a List-of-list-of-strings and hands this value to the latter.

This idea of composing a built-in function with a newly designed function is common. Naturally, people don’t design functions randomly and expect to find something in the chosen programming language to complement their design. Instead, program designers plan ahead and design the function to the output that available functions deliver. More generally still and as mentioned above, it is common to think about a solution as a composition of two computations and to develop an appropriate data collection with which to communicate the result of one computation to the second one, where each computation is each implemented with a function.

Exercise 157. Design a program that converts a list of lines into a string. The strings should be separated by blank spaces (" "). The lines should be separated with a newline ("\n").
Challenge: Remove all extraneous white spaces in your version of the Piet Hein poem. When you are finished with the design of the program, use it like this:
(write-file "ttt.dat" (collapse (read-words/line "ttt.txt")))
The two files "ttt.dat" and "ttt.txt" should be identical.

Exercise 158. Design a program that removes all articles from a text file. The program consumes the name n of a file, reads the file, removes the articles, and writes the result out to a file whose name is the result of concatenating "no-articles-" with n. For this exercise, an article is one of the following three words: "a", "an", and "the".
Use read-words/line so that the transformation retains the organization of the original text into lines and words. When the program is designed, run it on the Piet Hein poem.

Exercise 159. Design a program that encodes text files numerically. Each letter in a word should be encoded as a numeric three-letter string with a value between 0 and 256. Here is our encoding function for letters:
; 1String -> String
; convert the given 1string into a three-letter numeric string

; 1String -> String
; auxiliary for stating tests
(define (code1 c)
  (number->string (string->int c)))

(check-expect (encode-letter "\t") (string-append "00" (code1 "\t")))
(check-expect (encode-letter "a") (string-append "0" (code1 "a")))
(check-expect (encode-letter "z") (code1 "z"))

(define (encode-letter s)
  (cond
    [(< (string->int s) 10) (string-append "00" (code1 s))]
    [(< (string->int s) 100) (string-append "0" (code1 s))]
    [else (code1 s)]))
Before you start, explain this function. Also recall how a string can be converted into a list of 1Strings.
Again, use read-words/line to preserve the organization of the file into lines and words.

Exercise 160. Design a BSL program that simulates the Unix command wc. The purpose of the command is to count the number of characters (1Strings), words, and lines in a given file. That is, the command consumes the name of a file and produces a value that consists of three numbers.

Exercise 161. Mathematics teachers may have introduced you to matrix calculations by now. Numeric programs deal with those, too. Here is one possible data representation for matrices:
; A Matrix is one of:
; – empty
; – (cons LN Matrix)

; An LN is one of:
; – empty
; – (cons Number LN)

; interp. a matrix is a list of rows, a row is a list of numbers
; constraint: all rows are of the same length
Study it and translate the two-by-two matrix consisting of the numbers 11, 12, 21, 22 into this data representation. Stop, don’t read on until you have figured out the data examples.
Here is the solution for the five-second puzzle:
(define row1 (cons 11 (cons 12 empty)))
(define row2 (cons 21 (cons 22 empty)))
(define mat1 (cons row1 (cons row2 empty)))
If you didn’t create it yourself, study it now.
The following function implements the important mathematical operation of transposing the entries in a matrix. To transpose means to mirror the entries along the diagonal, that is, the line from the top-left to the bottom-right. Again, stop! Transpose mat1 by hand, then read on:
; Matrix -> Matrix
; transpose the items on the given matrix along the diagonal

(define wor1 (cons 11 (cons 21 empty)))
(define wor2 (cons 12 (cons 22 empty)))
(define tam1 (cons wor1 (cons wor2 empty)))

(check-expect (transpose mat1) tam1)

(define (transpose lln)
  (cond
    [(empty? (first lln)) empty]
    [else (cons (first* lln) (transpose (rest* lln)))]))
The definition assumes two auxiliary functions:
first*, which consumes a matrix and produces the first column as a list of numbers;
rest*, which consumes a matrix and removes the first column. The result is a matrix.
Even though you lack definitions for these functions, you should be able to understand how transpose works. You should also understand that you cannot design this function with the design recipes you have seen so far. Explain why.
Design the two “wish list” functions. Then complete the design of the transpose with some test cases.

11.4 Lists In Structures, Interactions

A Graphical Editor is about the design of an interactive graphical one-line editor. It suggests two different ways to represent the state of the editor and urges you to explore both: a structure that contains pair of strings or a structure that combines a string with an index to a current position (see exercise 76).

A third alternative is to use a structure type that combines two lists of 1Strings:

(define-struct editor (pre post))
; An Editor is (make-editor Lo1S Lo1S)
; An Lo1S is one of:
; – empty
; – (cons 1String Lo1S)

Before you wonder why, let us make up two data examples:

(define good
  (cons "g" (cons "o" (cons "o" (cons "d" empty)))))
(define all
  (cons "a" (cons "l" (cons "l" empty))))
(define lla
  (cons "l" (cons "l" (cons "a" empty))))

; data example 1:
(make-editor all good)

; data example 2:
(make-editor lla good)

The two examples demonstrate how important it is to write down an interpretation. While the two fields of an editor clearly represent the letters to the left and right of the cursor, the two examples demonstrate that there are at least two ways to interpret the structure types:

(make-editor pre post) could mean the letters in pre precede the cursor and those in post succeed it and that the combined text is
(string-append (implode pre) (implode post))
Recall that implode turns a list of 1Strings into a String.
(make-editor pre post) could equally well mean that the letters in pre precede the cursor in reverse order. If so, we obtain the text in the displayed editor like this:
(string-append (implode (rev pre)) (implode post))
The function rev must consume a list of 1Strings and produce their reverse.

Even without a complete definition for rev you can imagine how it works. Use this understanding to make sure you understand that translating the first data example into information according to the first interpretation and treating the second data example according to the second interpretation yields the same editor display:

Both interpretations are fine choices, but it turns out that using the second one greatly simplifies the design of the program. The rest of this subsection demonstrates this point, illustrating the use of lists inside of structures at the same time. To appreciate the lesson properly, you should have solved the exercises in A Graphical Editor.

Let us start with the design of rev, since we clearly need this function to make sense out of the data definition. Its header material is straightforward:

; Lo1s -> Lo1s
; produce a reverse version of the given list

(check-expect
  (rev (cons "a" (cons "b" (cons "c" empty))))
  (cons "c" (cons "b" (cons "a" empty))))

(define (rev l)
  l)

For good measure, we have added one “obvious” example as a test case. You may want to add some extra examples just to make sure you understand what is needed.

The template for rev is the usual list template:

(define (rev l)
  (cond
    [(empty? l) ...]
    [else (... (first l) ...
           ... (rev (rest l)) ...)]))

There are two cases, and the second case comes with several selector expressions and a self-referential one.

Filling in the template is easy for the first clause: the reverse version of the empty list is the empty list. For the second clause, we once again use the coding questions:

(first l) is the first item on the list of 1Strings;
(rest l) is the rest of the list; and
(rev (rest l)) is the reverse of the rest of the list.

Here is an illustration of the idea with the example from above:

l	(cons "a" (cons "b" (cons "c" empty)))
(first l)	"a"
(rest l)	(cons "b" (cons "c" empty))
(rev (rest l))	(cons "c" (cons "b" empty))

Since the desired result is

(cons "c" (cons "b" (cons "a" empty)))

we must somehow add "a" to the end of the result of the recursion. Indeed, if (rev (rest l)) is always the reverse of the rest of the list, it always suffices to add (first l) to its end. While we don’t have a function that adds items to the end of a list, we can wish for it and use it to complete the function definition:

(define (rev l)
  (cond
    [(empty? l) empty]
    [else (add-at-end (rev (rest l)) (first l))]))

Here is the extended wish list entry for add-at-end:

; Lo1s 1String -> Lo1s
; create a new list by adding s to the end of l

(check-expect
  (add-at-end (cons "c" (cons "b" empty)) "a")
  (cons "c" (cons "b" (cons "a" empty))))

(define (add-at-end l s)
  l)

It is “extended” because it comes with an example formulated as a test case. The example is derived from the example for rev, and indeed, it is precisely the example that motivates the wish list entry. Make up an example where add-at-end consumes an empty list before you read on.

Since add-at-end is also a list-processing function, the template is just a renaming of the one you know so well now:

(define (add-at-end l s)
  (cond
    [(empty? l) ...]
    [else (... (first l) ...
           ... (add-at-end (rest l) s) ...)]))

To complete it into a full function definition, we proceed according to the recipe questions for step 5. Our first question is to formulate an answer for the “basic” case, i.e., the first case here. If you did worked through the suggested exercise, you know that the result of

(add-at-end empty s)

is always (cons s empty). After all, the result must be a list and the list must contain the given 1String.

The next two questions concern the “complex” or “self-referential” case. We know what the expressions in the second cond line compute: the first expression extracts the first 1String from the given list and the second expression “creates a new list by adding s to the end of (rest l).” That is, the purpose statement dictates what the function must produce here. From here, it is clear that the function must add (first l) back to the result of the recursion:

(define (add-at-end l s)
  (cond
    [(empty? l) (cons s empty)]
    [else (cons (first l) (add-at-end (rest l) s))]))

Run the tests-as-examples to reassure yourself that this function works and that therefore rev works, too. Of course, you shouldn’t be surprised to find out that BSL already provides a function that reverses any given list, including lists of 1Strings. And naturally, it is called reverse.

Exercise 162. Design the function create-editor. The function consumes two strings and produces an Editor. The first string is the text to the left of the cursor and the second string is the text to the right of the cursor. The rest of the section relies on this function.

At this point, you should have a complete understanding of our data representation for the graphical one-line editor. Following the design strategy for interactive programs from Designing World Programs, you should define physical constants—the width and height of the editor, for example—and graphical constants—e.g., the cursor. Here are ours:

; constants
(define HEIGHT 20) ; the height of the editor
(define WIDTH 200) ; its width
(define FONT-SIZE 11) ; the font size
(define FONT-COLOR "black") ; the font color

; graphical constants
(define MT (empty-scene WIDTH HEIGHT))
(define CURSOR (rectangle 1 HEIGHT "solid" "red"))

The important point, however, is to write down the wish list for your event handler(s) and your function that draws the state of the editor. Recall that the "universe" teachpack dictates the header material for these functions:

; Editor -> Image
; render an editor as an image of the two texts separated by the cursor
(define (editor-render e)
MT)

; Editor KeyEvent -> Editor
; deal with a key event, given some editor
(define (editor-kh ed ke)
ed)

In addition, Designing World Programs demands that you write down a main function for your program:

; main : String -> Editor
; launch the editor given some initial string
(define (main s)
   (big-bang (create-editor s "")
             (on-key editor-kh)
             (to-draw editor-render)))

Re-read exercise 162 to understand what the initial editor for this program is.

While it doesn’t matter what you tackle next, we choose to design editor-kh first and editor-render second. Since we have the header material, let us explain the functioning of the key event handler with two examples:

(check-expect (editor-kh (create-editor "" "") "e")
(create-editor "e" ""))
(check-expect (editor-kh (create-editor "cd" "fgh") "e")
(create-editor "cde" "fgh"))

Both of these examples demonstrate what happens when you press the letter “e” on your keyboard. The computer runs the function editor-kh on the current state of the editor and "e". In the first example, the editor is empty, which means that the result is an editor with just the letter "e" in it followed by the cursor. In the second example, the cursor is between the strings "cd" and "fgh", and therefore the result is an editor with the cursor between "cde" and "fgh". In short, the function always inserts any normal letter at the cursor position.

Before you read on, you should make up examples that illustrate how editor-kh works when you press the backspace ("\b") key to delete some letter, the "left" and "right" arrow keys to move the cursor, or some other arrow keys. In all cases, consider what should happen when the editor is empty, when the cursor is at the left end or right end of the non-empty string in the editor, and when it is in the middle. Even though you are not working with intervals here, it is still a good idea to develop examples for the “extreme” cases.

Once you have test cases, it is time to develop the template. In the case of editor-kh you are working with a function that consumes two complex forms of data: one is a structure containing lists, the other one is a large enumeration of strings. Generally speaking, the use of two complex inputs calls for a special look at the design recipe; but in cases like these, it is also clear that you should deal with one of the inputs first, namely, the keystroke.

Having said that, the template is just a large cond expression for checking which KeyEvent the function received:

(define (editor-kh ed k)
  (cond
    [(key=? k "left") ...]
    [(key=? k "right") ...]
    [(key=? k "\b") ...]
    [(key=? k "\t") ...]
    [(key=? k "\r") ...]
    [(= (string-length k) 1) ...]
    [else ...]))

The cond expression doesn’t quite match the data definition for KeyEvent because some KeyEvents need special attention (for example ("left", "right", "\b"); some need to be ignored ("\t" and "\r") because they are special; and some should be classified into one large group (ordinary keys).

Exercise 163. Explain why the template for editor-kh deals with "\t" and "\r" before it checks for strings of length 1.

For the fifth step—the definition of the function—we tackle each clause in the conditional separately. The first clause demands a result that moves the cursor and leaves the string content of the editor alone. So does the second clause. The third clause, however, demands the deletion of a letter from the editor’s content—if there is a letter. Last but not least, the sixth cond clause concerns the addition of letters at the cursor position. Following the first basic guideline, we make extensive use of a wish list and imagine one function per task:

(define (editor-kh ed k)
  (cond
    [(key=? k "left") (editor-lft ed)]
    [(key=? k "right") (editor-rgt ed)]
    [(key=? k "\b") (editor-del ed)]
    [(key=? k "\t") ed]
    [(key=? k "\r") ed]
    [(= (string-length k) 1) (editor-ins ed k)]
    [else ed]))

As you can tell from the definition of editor-kh, three of the four wish list functions have the same signature:

; Editor -> Editor

The last one takes two arguments instead of one:

; Editor 1String -> Editor

We leave the proper formulation of wishes for the first three functions to you and focus on the fourth one.

Let us start with a purpose statement and a function header:

; insert the 1String k between pre and post
(define (editor-ins ed k)
ed)

The purpose is straight out of the problem statement. For the construction of a function header, we need an instance of Editor. Since pre and post are the pieces of the current one, we just put them back together.

Next we derive some examples for editor-ins from the examples for editor-kh:

(check-expect
  (editor-ins (make-editor empty empty) "e")
  (make-editor (cons "e" empty) empty))

(check-expect
  (editor-ins (make-editor (cons "d" empty)
                           (cons "f" (cons "g" empty)))
              "e")
  (make-editor (cons "e" (cons "d" empty))
               (cons "f" (cons "g" empty))))

You should work through these examples using the interpretation of Editor. That is, make sure you understand what the given editor means as information and what the function call is supposed to achieve in terms of information. In this particular case, it is best to draw the visual representation of the editor because it is the information of that we have in mind.

The fourth step demands the development of the template. The first argument is guaranteed to be a structure, and the second one is a string, an atomic piece of data. In other words, the template just pulls out the pieces from the given editor representation:

(define (editor-ins ed k)
(... ed ... k ... (editor-pre ed) ... (editor-post ed) ...))

As a reminder that the parameters are available too, we have added them to the template body.

From the template and the examples, it is relatively easy to conclude what editor-ins is supposed to create an editor from the given editor’s pre and post fields with k added to the front of the former:

(define (editor-ins ed k)
(make-editor (cons k (editor-pre ed)) (editor-post ed)))

Even though both (editor-pre ed) and (editor-post ed) are list of 1Strings, there is clearly no need to design auxiliary functions. To get the desired result, it suffices to use the simplest built-in functions for lists: cons, which creates lists.

At this point, you should do two things. First, run the tests for this function. Second, use the interpretation of Editor and explain abstractly why this function performs the insertion. And if this isn’t enough, you may wish to compare this simple definition with the one from exercise 73 and figure out why the other one needs an auxiliary function while our definition here doesn’t.

Exercise 164. Design the functions
; Editor -> Editor
; move the cursor position one 1String left, if possible
(define (editor-lft ed)
  ed)

; Editor -> Editor
; move the cursor position one 1String right, if possible
(define (editor-rgt ed)
  ed)

; Editor -> Editor
; delete one 1String to the left of the cursor, if possible
(define (editor-del ed)
  ed)
Again, it is critical that you work through a good range of examples.

Designing the rendering function for Editors poses some new but small challenges. The first one is to develop a sufficiently large number of test cases. On one hand, it demands coverage of the possible combinations: an empty string to the left of the cursor, an empty one on the right, and both strings empty. On the other hand, it also requires some experimenting with the functions that the image library provides. Specifically, it needs a way to juxtapose the two pieces of strings rendered as text images; and it needs a way of placing the text image into the empty image frame (MT). Here is what we do to create an image for the result of (create-editor "pre" "post"):

(place-image/align
  (beside (text "pre" FONT-SIZE FONT-COLOR)
          CURSOR
          (text "post" FONT-SIZE FONT-COLOR))
  1 1
  "left" "top"
  MT)

If you compare this with the editor image above, you notice some differences, which is fine because the exact layout isn’t essential to the purpose of this exercise, and because the revised layout doesn’t trivialize the problem. In any case, do experiment in the interactions area of DrRacket to find your favorite editor display.

You are now ready to develop the template, and you should come up with this much:

(define (editor-render e)
(... (editor-pre e) ... (editor-post e)))

The given argument is just a structure type with two fields. Their values, however, are lists of 1Strings, and you might be tempted to refine the template even more. Don’t! Instead, keep in mind that when one data definition refers to another, complex data definition, you are better off using the wish list.

If you have worked through a sufficient number of examples, you also know what you want on your wish list: one function that turns a string into a text of the right size and color. Let us call this function editor-text. Then the definition of editor-render just uses editor-text twice and then composes the result with beside and place-image:

; Editor -> Image
(define (editor-render e)
  (place-image/align
    (beside (editor-text (editor-pre e))
            CURSOR
            (editor-text (editor-post e)))
    1 1
    "left" "top"
    mt))

Although this definition nests expressions three levels deep, the use of the imaginary editor-text function renders it quite readable.

What remains is to design editor-text. From the design of editor-render, we know that editor-text consumes a list of 1Strings and produces a text image:

; Lo1s -> Image
; render a list of 1Strings as a text image
(define (editor-text s)
(text "" FONT-SIZE FONT-COLOR))

The header here produces an empty string, using the defined font size and font color.

To demonstrate what editor-text is supposed to compute, we work through an example derived from the example for editor-render. The example input is

(create-editor "pre" "post")

which is equivalent to

(make-editor
(cons "e" (cons "r" (cons "p" empty)))
(cons "p" (cons "o" (cons "s" (cons "t" empty)))))

We pick the second list as our sample input for editor-text, and we know the expected result from the example for editor-render:

(check-expect
(editor-text (cons "p" (cons "o" (cons "s" (cons "t" empty)))))
(text "post" FONT-SIZE FONT-COLOR))

You may wish to make up a second example before reading on.

Given that editor-text consumes a list of 1Strings, we can write down the template without much ado:

(define (editor-text s)
  (cond
    [(empty? s) ...]
    [else (... (first s)
           ... (editor-text (rest s)) ...)]))

After all, the template is dictated by the data definition that describes the function input. But you don’t need the template if you understand and keep in mind the interpretation for Editor. It uses explode to turn a string into a list of 1Strings. Naturally, there is a function implode that performs the inverse computation, i.e.,

> (implode (cons "p" (cons "o" (cons "s" (cons "t" empty)))))
"post"

Using this function, the definition of editor-text is just a small step from the example to the function body:

(define (editor-text s)
(text (implode s) FONT-SIZE FONT-COLOR))

Exercise 165. Just because we recalled implode, you may not do so when you need to. It turns out that it is also possible to finish the design of editor-text without implode, following the same old guidelines we have used so many times. You may need one hint though, because you may not expect this: (circle 0 "solid" "red") creates an “empty” or “invisible” image.

The true surprise comes when you test the two functions. While our test for editor-text succeeds, the test for editor-render fails. An inspection of the failure shows that the string to the left of the cursor— "pre"—is type-set backwards. We forgot to remember that this part of the editor’s state is represented in reverse. Conversely, when we render it, we need to reverse it again. Fortunately, the unit tests for the two functions pinpoint which function is wrong and even tell us what is wrong with the function. The fix is trivial:

(define (editor-render e)
  (place-image/align
    (beside (editor-text (reverse (editor-pre e)))
            CURSOR
            (editor-text (editor-post e)))
    1 1
    "left" "top"
    mt))

It uses the reverse function on the pre field of e.

12 Design By Composition

This last chapter of part II covers “design by composition.” By now you know that programs are complex products and that their production requires the design of many collaborating functions. This collaboration work well if the designer knows when to design several functions and how to compose these functions into one program.

You have encountered this need to design interrelated functions several times. Sometimes a problem statement implies several different tasks, and each task is best realized with a function. At other times, a data definition may refer to another one, and in that case, a function processing the former kind of data relies on a function processing the latter.

In this chapter, we present yet other scenarios that call for the design of many functions and their composition. To support this kind of work, the chapter presents some informal guidelines on divvying up functions and composing them. The next chapter then introduces some well-known examples whose solutions rely on the use of these guidelines and the design recipe in general. Since these examples demand complex forms of lists, however, this chapter starts with a section on a convenient way to write down complex lists.

12.1 The list function

At this point, you should have tired of writing so many conses just to create a list, especially for lists that contain a bunch of values. Fortunately, Racket—the language from which our teaching languages originate—provides mechanisms for simplifying this part of a programmer’s life. BSL+Yes, you have graduated from BSL. It is time to use the “Language” menu and to select the “Choose Language” entry. From now until further notice, use “Beginning Student Language with List Abbreviations” to work through the book. does so, too.

The key innovation is the list operation, which consumes an arbitrary number of values and creates a list. The simplest way to understand list expressions is to think of them as abbreviations. Specifically, every expression of the shape

(list exp-1 ... exp-n)

stands for a series of n cons expressions:

(cons exp-1 (cons ... (cons exp-n empty)))

Keep in mind that empty is not an item of the list here, but the rest of the list. Here is a table with three examples:

short-hand
long-hand

(list "ABC")
(cons "ABC" empty)

(list false true)
(cons false (cons true empty))

(list 1 2 3)
(cons 1 (cons 2 (cons 3 empty)))

They introduce lists with one, two, and three items, respectively.

Of course, we can apply list not only to values but also to expressions:

> (list (+ 0 1) (+ 1 1))
(list 1 2)
> (list (/ 1 0) (+ 1 1))
/: division by zero

Before the list is constructed, the expressions must be evaluated. If during the evaluation of an expression an error occurs, the list is never formed. In short, list behaves just like any other primitive operation that consumes an arbitrary number of arguments; its result just happens to be a list constructed with conses.

The use of list greatly simplifies the notation for lists with many items and lists that contains lists or structures. Here is an example:

(list 0 1 2 3 4 5 6 7 8 9)

This list contains 10 items and its formation with cons would require 10 uses of cons and one instance of empty. Similarly, the list

(list (list "bob" 0 "a")
      (list "carl" 1 "a")
      (list "dana" 2 "b")
      (list "erik" 3 "c")
      (list "frank" 4 "a")
      (list "grant" 5 "b")
      (list "hank" 6 "c")
      (list "ian" 8 "a")
      (list "john" 7 "d")
      (list "karel" 9 "e"))

requires 11 uses of list, which sharply contrasts with 40 cons and 11 additional uses of empty.

Exercise 166. Use list to construct the equivalent of the following lists:
(cons "a" (cons "b" (cons "c" (cons "d" (cons "e" empty)))))
(cons (cons 1 (cons 2 empty)) empty)
(cons "a" (cons (cons 1 empty) (cons false empty)))
(cons (cons 1 (cons 2 empty)) (cons (cons 2 empty) empty))
(cons (cons "a" (cons 2 empty)) (cons "hello" empty))
Start by determining how many items each list and each nested list contains. Use check-expect to express your answers; this ensures that your abbreviations are really the same as the long-hand.

Exercise 167. Use cons and empty to construct the equivalent of the following lists:
(list 0 1 2 3 4 5)
(list (list "adam" 0) (list "eve" 1) (list "louisXIV" 2))
(list 1 (list 1 2) (list 1 2 3))
Use check-expect to express your answers.

Exercise 168. On some occasions lists are formed with cons and list. Reformulate the following lists using cons and empty exclusively:
(cons "a" (list 0 false))
(list (cons 1 (cons 13 empty)))
(cons (list 1 (list 13 empty)) empty)
(list empty empty (cons 1 empty))
(cons "a" (cons (list 1) (list false empty)))
Then formulate the lists using only list. Use check-expect to express your answers.

Exercise 169. Determine the values of the following expressions:
(list (string=? "a" "b") (string=? "c" "c") false)
(list (+ 10 20) (* 10 20) (/ 10 20))
(list "dana" "jane" "mary" "laura")
Use check-expect to express your answers.

Exercise 170. You know about first and rest from BSL, but BSL+ comes with even more selectors than that. Determine the values of the following expressions:
(first (list 1 2 3))
(rest (list 1 2 3))
(second (list 1 2 3))
Find out from the documentation whether third, fourth, and fifth exist.

12.2 Composing Functions

How To Design Programs explains that programs are collections of definitions: structure type definitions, data definitions, constant definitions, and function definitions.And don’t forget tests. To guide the division of labor among functions, the section also suggests a rough guideline:

Formulate auxiliary function definitions for every dependency between quantities in the problem statement. In short, design one function per task.

This part of the book introduces another guideline on auxiliary functions:

Formulate auxiliary function definitions when one data definition points to a second data definition. Roughly, design one template per data definition.

In this section, we take a look at one specific place in the design process that may call for additional auxiliary functions: the definition step, which creates a full-fledged definition from a template. Turning a template into a complete function definition means combining the values of the template’s subexpressions into the final answer. As you do so, you might encounter several situations that suggest the need for auxiliary functions:

If the composition of values requires knowledge of a particular domain of application—for example, composing two (computer) images, accounting, music, or science—design an auxiliary function.
If the composition of values requires a case analysis of the available values—for example, is a number positive, zero, or negative— use a cond expression. If the cond looks complex, design an auxiliary function whose inputs are the partial results and whose function body is the cond expression. Doing so separates out the case analysis from the recursive process.
If the composition of values must process an element from a self-referential data definition—a list, a natural number, or something like those—design an auxiliary function.
If everything fails, you may need to design a more general function and define the main function as a specific use of the general function. This suggestion sounds counter-intuitive but it is called for in a remarkably large number of cases.

The last two criteria are situations that we haven’t discussed in any detail, though examples have come up before. The next two sections illustrate these principles with additional examples.

Before we move forward, though, remember that the key to managing the design of many functions and their compositions is to maintain the often-mentioned

Wish Lists

Maintain a list of function headers that must be designed to complete a program. Writing down complete function headers ensures that you can test those portions of the programs that you have finished, which is useful even though many tests will fail. Of course, when the wish list is empty, all tests should pass and all functions should be covered by tests.

Before you put a function on the wish list, you should check whether something like the function already exists in your language’s library or whether something similar is already on the wish list. BSL, BSL+, and indeed all programming languages provide many built-in operations and many library functions. You should explore your chosen language when you have time and when you have a need, so that you know what it provides.

12.3 Recursive Auxiliary Functions

People need to sort things all the time, and so do programs. Investment advisors sort portfolios by the profit each holding generates. Game programs sort lists of players according to scores. And mail programs sort messages according to date or sender or some other criteria.

In general, you can sort a bunch of items if you can compare and order each pair of data items. Although not every kind of data comes with a comparison primitive, we all know one that does: numbers. Hence, we use a simplistic but highly representative sample problem in this section:

Sample Problem: Design a function that sorts a list of (real) numbers.

The exercises of this section clarify how to adapt this design to other forms of data.

Since the problem statement doesn’t mention any other task and since sorting doesn’t seem to suggest other tasks, we just follow the design recipe. Sorting means rearranging a bunch of numbers. This re-statement implies a natural data definition for the inputs and outputs of the function and thus its signature. Given that we have a definition for List-of-numbers, the first step is easy:

; List-of-numbers -> List-of-numbers
; produces a sorted version of alon
(define (sort-> alon)
alon)

Returning alon ensures that the result is appropriate as far as the function signature is concerned, but in general, the given list isn’t sorted and this result is wrong.

When it comes to making up examples, it quickly becomes clear that the problem statement is quite imprecise. As before, we use the data definition of List-of-numbers to organize the development of examples. Since the data definition consists of two clauses, we need two examples. Clearly, when sort-> is applied to empty, the result must be empty. The question is what the result for

(cons 12 (cons 20 (cons -5 empty)))

should be. The list isn’t sorted, but there are two ways to sort it:

(cons 20 (cons 12 (cons -5 empty))), i.e., a list with the numbers arranged in descending order; and
(cons -5 (cons 12 (cons 20 empty))), i.e., a list with the numbers arranged in ascending order.

In a real-world situation, you would now have to ask the person who posed the problem for clarification. Here we go for the descending alternative; designing the ascending alternative doesn’t pose any different obstacles.

The decision calls for a revision of the header material:

; List-of-numbers -> List-of-numbers
; produces a version of alon, sorted in descending order

(check-expect (sort-> empty) empty)

(check-expect (sort-> (list 12 20 -5)) (list 20 12 -5))

(check-expect (sort-> (list 3 2 1)) (list 3 2 1))

(check-expect (sort-> (list 1 2 3)) (list 3 2 1))

(define (sort-> alon)
alon)

The header material now includes the examples reformulated as unit tests and using list. If the latter makes you uncomfortable, reformulate the test with cons to exercise translating back and forth. As for the additional two examples, they demand that sort works on lists sorted in ascending and descending order.

Next we must translate the data definition into a function template. We have dealt with lists of numbers before, so this step is easy:

(define (sort-> alon)
  (cond
    [(empty? alon) ...]
    [else (... (first alon) ... (sort-> (rest alon)) ...)]))

Using this template, we can finally turn to the interesting part of the program development. We consider each case of the cond expression separately, starting with the simple case. If sort->’s input is empty, the answer is empty, as specified by the example. If sort->’s input is a consed list, the template suggests two expressions that might help:

(first alon) extracts the first number from the input;
(sort-> (rest alon)) produces a sorted version of (rest alon), according to the purpose statement of the function.

To clarify these abstract answers, let us use the second example to explain these pieces in detail. When sort-> consumes (list 12 20 -5),

(first alon) is 12,
(rest alon) is (list 20 -5), and
(sort-> (rest alon)) produces (list 20 -5), because this list is already sorted.

To produce the desired answer, sort-> must insert 12 between the two numbers of the last list. More generally, we must find an expression that inserts (first alon) in its proper place into the result of (sort-> (rest alon)). If we can do so, sorting is an easily solved problem.

Inserting a number into a sorted list clearly isn’t a simple task. It demands searching through the sorted list to find the proper place of the item. Searching through any list, however, demands an auxiliary function, because lists are of arbitrary size and, by hint 3 of the preceding section, processing values of arbitrary calls for the design of an auxiliary function.

So here is the new wish list entry:

; Number List-of-numbers -> List-of-numbers
; insert n into the sorted list of numbers alon
(define (insert n alon)
alon)

That is, insert consumes a number and a list sorted in descending order and produces a sorted list by inserting the former into the right place in the latter.

Using insert, it is easy to complete the definition of sort->:

(define (sort-> alon)
  (cond
    [(empty? alon) empty]
    [else (insert (first alon) (sort-> (rest alon)))]))

The second clause says that, in order to produce the final result, sort-> extracts the first item of the non-empty list, computes the sorted version of the rest of the list, and uses insert to produce the completely sorted list from the two pieces.

Before you read on, test the program. You will see that some test cases pass and some fail. That is progress but clearly, we are not really finished until we have developed insert. The next step in its design is the creation of functional examples. Since the first input of insert is any number, we use 5 and use the data definition for List-of-numbers to make up examples for the second input. First we consider what insert should produce when given a number and empty. According to insert’s purpose statement, the output must be a list, it must contain all numbers from the second input, and it must contain the first argument. This suggests the following:

(check-expect (insert 5 empty) (list 5))

Instead of 5, we could have used any number.

Second, we use a non-empty list of just one item:

(check-expect (insert 5 (list 6)) (list 6 5))
(check-expect (insert 5 (list 4)) (list 5 4))

The reasoning of why these are the expected results is just like before. For one, the result must contain all numbers from the second list and the extra number. For two, the result must be sorted.

Finally, let us create an example with a list that contains more than one item. Indeed, we can derive such an example from the examples for sort-> and especially from our analysis of the second cond clause. From there, we know that sort-> works only if 12 is inserted into (list 20 -5) at its proper place:

(check-expect (insert 12 (list 20 -5)) (list 20 12 -5))

That is, insert is given a second list and it is sorted in descending order.

Note what the development of examples teaches us. The insert function has to find the first number that is smaller than the given n. When there is no such number, the function eventually reaches the end of the list and it must add n to the end. Now, before we move on to the template, you should work out some additional examples. To do so, you may wish to use the supplementary examples for sort->.

In contrast to sort->, the function insert consumes two inputs. Since we know that the first one is a number and atomic, we can focus on the second argument—the list of numbers—for the template development:

(define (insert n alon)
  (cond
    [(empty? alon) ...]
    [else (... (first alon) ... (insert n (rest alon)) ...)]))

The only difference between this template and the one for sort-> is that this one needs to take into account the additional argument n.

To fill the gaps in the template of insert, we again proceed on a case-by-case basis. The first case concerns the empty list. According to the first example, (list n) is the expression needed in the first cond clause, because it constructs a sorted list from n and alon.

The second case is more complicated than the first, and so we follow the questions from figure 38:

(first alon) is the first number on alon, and
(rest alon) is the rest of alon and, like alon, it is sorted in descending order;
(insert n (rest alon)) produces a sorted list from n and the numbers on (rest alon).

The problem is how to combine these pieces of data to get the final answer.

Let us work through some examples to make all this concrete:

(insert 7 (list 6 5 4))

Here n is 7 and larger than any of the numbers in the second input. We know so by just looking at the first item of the list. It is 6 but because the list is sorted, all other numbers on the list are even smaller than 6. Hence it suffices if we just cons 7 onto (list 6 5 4).

In contrast, when the application is something like

(insert 0 (list 6 2 1 -1))

n must indeed be inserted into the rest of the list. More concretely, (first alon) is 6; (rest alon) is (list 2 1 -1); and (insert n (rest alon)) produces (list 2 1 0 -1) according to the purpose statement. By adding 6 back onto that last list, we get the desired answer for (insert 0 (list 6 2 1 -1)).

To get a complete function definition, we must generalize these examples. The case analysis suggests a nested conditional that determines whether n is larger than (or equal to) (first alon):

If so, all the items in alon are smaller than n because alon is already sorted. The answer in that case is (cons n alon).
If, however, n is smaller than (first alon), then the function has not yet found the proper place to insert n into alon. The first item of the result must be (first alon) and that n must be inserted into (rest alon). The final result in this case is
(cons (first alon) (insert n (rest alon)))
because this list contains n and all items of alon in sorted order—which is what we need.

The translation of this discussion into BSL+ calls for an if expression for such cases. The condition is (>= n (first alon)) and the expressions for the two branches have been formulated.

Figure 46 contains the complete definitions of insert and sort->. Copy it into the definition area of DrRacket, add the test cases back in, and test the program. All tests should pass now and they should cover all expressions.

Terminology This particular program for sorting is known as insertion sort in the programming literature. Later we will study alternative ways to sort lists, using an entirely different design strategy.

; List-of-numbers -> List-of-numbers
; produces a sorted version of alon
(define (sort-> alon)
  (cond
    [(empty? alon) empty]
    [(cons? alon) (insert (first alon) (sort-> (rest alon)))]))

; Number List-of-numbers -> List-of-numbers
; insert n into the sorted list of numbers alon
(define (insert n alon)
  (cond
    [(empty? alon) (cons n empty)]
    [else (if (>= n (first alon))
              (cons n alon)
              (cons (first alon) (insert n (rest alon))))]))
Figure 46: Sorting lists of numbers

Exercise 171. Design a program that sorts lists of email messages by date:
(define-struct email (from date message))
; A Email Message is a structure:
; – (make-email String Number String)
; interp. (make-email f d m) represents text m sent by
; f, d seconds after the beginning of time
Also develop a program that sorts lists of email messages by name. To compare two strings alphabetically, use the string<? primitive.

Exercise 172. Design a program that sorts lists of game players by score:
(define-struct gp (name score))
; A GamePlayer is a structure:
; – (make-gp String Number)
; interp. (make-gp p s) represents player p who scored
; a maximum of s points

Exercise 173. Here is the function search:
; Number List-of-numbers -> Boolean
(define (search n alon)
  (cond
    [(empty? alon) false]
    [else (or (= (first alon) n) (search n (rest alon)))]))
It determines whether some number occurs in a list of numbers. The function may have to traverse the entire list to find out that the number of interest isn’t contained in the list.
Develop the function search-sorted, which determines whether a number occurs in a sorted list of numbers. The function must take advantage of the fact that the list is sorted.

12.4 Generalizing Functions

Auxiliary functions are also needed when a problem statement is too narrow. Conversely, it is common for programmers to generalize a given problem just a bit to simplify the solution process. When they discover the need for a generalized solution, they design an auxiliary function that solves the generalized problem and a main function that just calls this auxiliary function with special arguments.

We illustrate this idea with a solution for the following problem: Mr. Paul C. Fisher inspired the use of this problem.

Sample Problem: Design a program that renders a polygon into an empty 50 by 50 scene.

Just in case you don’t recall your basic geometry (domain) knowledge, we add one definition of polygon:

A polygon is a planar figure with at least three corners consecutively connected by three straight sides. And so on.

One natural data representation for a polygon is thus a list of Posns where each one represents the coordinates of one corner. For example,

(list (make-posn 10 10)
(make-posn 60 60)
(make-posn 10 60))

represents a triangle. You may wonder what empty or (list (make-posn 30 40)) mean as a polygon and the answer is that they do not describe polygons, and neither do lists with two Posns.

As the domain knowledge statement says, a polygon consists of at least three sides and that means at least three Posns. Thus the answer to our question is that representations of polygons should be lists of at least three Posns.

Following the development of the data definition for NEList-of-temperatures in Non-empty Lists, formulating a data representation for polygons is straightforward:

; a Polygon is one of:
; – (list Posn Posn Posn)
; – (cons Posn Polygon)

The first clause says that a list of three Posns is a Polygon and the second clause says that consing another Posn onto some existing Polygon creates another one. Since this data definition is the very first to use list in one of its clauses, we spell it out with cons just to make sure you see this conversion from an abbreviation to long hand in this context:

; a Polygon is one of:
; – (cons Posn (cons Posn (cons Posn empty)))
; – (cons Posn Polygon)

The point of this discussion is that a naively chosen data representation—lists of Posns—may not properly represent the intended information. Revising the data definition during such an exploration is a normal step; indeed, on occasion such revisions become necessary during the rest of the design process. As long as you stick to a systematic approach, though, changes to the data definition can naturally be propagated through the rest of the program design.

The second step calls for the signature, purpose statement, and header of the program. Since the problem statement mentions just one task and no other task is implied, we start with one function:

(define MT (empty-scene 50 50))

; Polygon -> Image
; to render the given polygon p into MT
(define (render-poly p)
MT)

The separate definition of MT is also called for, considering that the empty scene is mentioned in the problem statement and that it is going to be needed to formulate examples.

For the first example, we use the above-mentioned triangle. A quick look in the "2htdp/image" teachpack suggests add-line is the function needed to render the three lines for a triangle:

(check-expect
  (render-poly
    (list (make-posn 20 0) (make-posn 10 10) (make-posn 30 10)))
  (add-line
    (add-line
      (add-line MT 20 0 10 10 "red")
      10 10 30 10 "red")
    30 10 20 0 "red"))

The innermost add-line render the line from the first to the second Posn; the middle one uses the second and third Posn; and the outermost add-line connects the third and the first Posn. Of course, we experimented in DrRacket’s interaction area to get this expression right, and you should, too.

Given that the first and smallest polygon is a triangle, a rectangle or a square suggests itself as the second example:

(check-expect
  (render-poly
    (list (make-posn 10 10) (make-posn 20 10)
          (make-posn 20 20) (make-posn 10 20)))
  (add-line
    (add-line
      (add-line
        (add-line MT 10 10 20 10 "red")
        20 10 20 20 "red")
      20 20 10 20 "red")
    10 20 10 10 "red"))

Both add just one corner to triangles and both are easy to render. You may also wish to draw these shapes on a piece of graph paper before you experiment.

The construction of the template poses a serious challenge. Specifically, the first and the second question of figure 36 ask whether the data definition differentiates distinct subsets and how to distinguish among them. While the data definition clearly sets apart triangles from all other polygons in the first clause, it is not immediately clear how to differentiate the two. Both clauses describe lists of Posns. The first describes lists of three Posns, the second one describes lists of Posns that have at least four items. Thus one alternative is to ask whether the given polygon is three items long:

(= (length p) 3)

Using the long-hand version of the first clause, i.e.,

(cons Posn (cons Posn (cons Posn empty)))

suggests a second way to formulate the condition, namely, checking whether the given Polygon is empty after using three rest functions:

(empty? (rest (rest (rest p))))

Since all Polygons consist of at least three Posns, using rest three times is legal. Unlike length, rest is also a primitive, easy-to-understand operation with a clear operational meaning. It selects the second field in a cons structure and that is all it does.

In general, it is better to formulate conditions in via built-in predicates and selectors than your own (recursive) functions. We will explain this remark in detail later.

The rest of the questions in figure 36 have direct answers, and thus we get this template:

(define (render-poly p)
  (cond
    [(empty? (rest (rest (rest p))))
     (... (first p) ... (second p) ... (third p) ...)]
    [else ( ... (first p) ... (render-poly (rest p)) ...)]))

Because p in the first clause describes a triangle, we know that it consists of exactly three Posns, which are selected via first, second, and third. Furthermore, p in the second clause consists of a Posn and a Polygon, justifying (first p) and (rest p). The former extracts a Posn from p, the latter a Polygon. We therefore add a self-referential function call around the latter; we should also keep in mind that dealing with (first p) in this clause and the three Posns in the first clause may demand the design of an auxiliary function.

Now we are ready to focus on the function definition, dealing with one clause at a time. The first clause concerns triangles, which in turn suggests a relatively straightforward solution. Specifically, there are three Posns and render-poly should connect the three in an empty scene of 50 by 50 pixels. Given Posn is a separate data definition, we get an obvious wish list entry:

; Image Posn Posn -> Image
; draw a red line from Posn p to Posn q into im
(define (render-line im p q)
im)

Using this function, the first cond clause in render-poly can easily create an answer like this:

(render-line
  (render-line
    (render-line MT (first p) (second p))
    (second p) (third p))
  (third p) (first p))

This expression obviously renders the given Polygon p as a triangle by drawing a line from the first to the second, the second to the third, and the third to the first Posn.

The second cond clause is about Polygons that have been extended with one additional Posn. In the template, we find two expressions and, following figure 38, we remind ourselves of what these expressions compute:

(first p) extracts the first Posn;
(rest p) extracts the Polygon from p; and
(render-polygon (rest p)) renders the Polygon extracted by (rest p) in MT.

The question is how to use these pieces to render the originally given Polygon p.

One idea that may come to mind is that (rest p) consists of at least three Posns. It is therefore possible to extract at least one Posn from this embedded Polygon and to connect (first p) with this additional point. Here is what this idea looks like with BSL+ code:

(render-line (render-poly (rest p)) (first p) (second p))

As mentioned, the fragment on a dark background renders the embedded Polygon in an empty 50 by 50 scene. The use of render-line adds one line to this scene, from the first to the second Posn of p.

Our suggestions imply the following complete function definition:

(define (render-poly p)
  (cond
    [(empty? (rest (rest (rest p))))
     (render-line
       (render-line
         (render-line MT (first p) (second p))
         (second p) (third p))
       (third p) (first p))]
    [else
      (render-line
        (render-poly (rest p)) (first p) (second p))]))

Designing render-line is a problem that you solved in the first part of the book, so we just provide the final definition so that you can test the program:

; Image Posn Posn -> Image
; render a line from Posn p to Posn q into im
(define (render-line im p q)
(add-line
im (posn-x p) (posn-y p) (posn-x q) (posn-y q) "red"))

Sixth and last, we must test the functions. You should add a test for render-line but for now you may just accept our correctness promise. In that case, testing immediately reveals flaws with the definition of render-poly; in particular, the test case for the square fails. On one hand, this is fortunate because it is the purpose of tests to find problems before they affect regular consumers. On the other hand, the flaw is unfortunate because we followed the design recipe, we made fairly regular decisions, and yet the function doesn’t work.

Before you give up hope in such a situation, you should experiment with the function in DrRacket’s interactions area. For our example, the results are illuminating. Here is the failing test case, with the input on the left and the output on the right:

p

(render-polygon p)

(list (make-posn 10 10)
      (make-posn 20 10)
      (make-posn 20 20)
      (make-posn 10 20))

To highlight the problems, we have added visible dots for the four given Posns. As you can see, the image on the right shows that render-polygon connects the three dots of (rest p) and then connects (first p) to the first point of (rest p), i.e., (second p).

You can easily validate this claim with an interaction that uses (rest p) directly as input for render-poly:

p

(render-polygon p)

(list (make-posn 20 10)
(make-posn 20 20)
(make-posn 10 20))

And the result is indeed the triangle of the image above.

In addition, you may wonder what render-poly would do if we extended the original square with another point, say, (make-posn 10 5).

p

(render-polygon p)

(list (make-posn 10 5)
      (make-posn 10 10)
      (make-posn 20 10)
      (make-posn 20 20)
      (make-posn 10 20))

Instead of a polygon, render-polygon always draws the triangle at the end of the given Polygon and otherwise connects the Posns that precede the triangle.

As a matter of fact, one could also argue that render-polygon is really the function that connects the successive dots specified by a list of Posns and connects the first and the last Posn of the trailing triangle. If we don’t draw this last, extra line, render-polygon is just a “connects the dots” function. And as such, it almost solves our original problem; all that is left to do is to add a line from the first Posn to the last one in the given Polygon.

Put differently, the analysis of our failure suggests two ideas at once. First, we should solve a different, a more general looking problem. Second, we should use the solution for this generalized problem to solve the original one.

We start with the statement for the general problem:

Sample Problem: Design a program that connects a bunch of dots.

Although the design of render-poly almost solves this problem, we design this function mostly from scratch. First, we need a data definition. Connecting the dots makes no sense unless we have at least one dot or two. To make things simple, we go with the first alternative:

; A NELoP is one of:
; – (cons Posn empty)
; – (cons Posn NELoP)

The organization of this data definition should be familiar from Non-empty Lists. In that section, the definition for NEList-of-temperatures describes lists that contain at least one temperature; here NELoP introduces the collection of lists of Posns with at least one Posn.

Second, we formulate a signature, a purpose statement, and a header for a “connect the dots” function:

; NELoP -> Image
; connect the dots in p by rendering lines in MT
(define (connect-dots p)
MT)

Third, we adapt the examples for render-poly for this new function. As our failure analysis says, the function connects the first Posn on p to the second one, the second one to the third, the third to the fourth, and so on, all the way to the last one, which isn’t connected to anything. Here is the adaptation of the first example, a list of three Posns:

(check-expect (connect-dots (list (make-posn 20 0)
                                  (make-posn 10 10)
                                  (make-posn 30 10)))
              (add-line
               (add-line MT 20 0 10 10 "red")
               10 10 30 10 "red"))

The expected value is an expression that adds two lines to MT: one line from the first Posn to the second one, and another line from the second to the third Posn.

Exercise 174. Adapt the second example for render-poly to connect-dots.

Fourth, we use the template for functions the process non-empty lists:

(define (connect-dots p)
  (cond
    [(empty? (rest p)) (... (first p) ...)]
    [else (... (first p) ... (connect-dots (rest p)) ...)]))

The template has two clauses: one for lists of one Posn and the second one for lists with more than one. Since there is at least one Posn in both cases, the template contains (first p) in both clauses; the second one also contains (connects-dots (rest p)) to remind us of the self-reference in the second clause of the data definition.

The fifth and central step is to turn the template into a function definition. Since the first clause is the simplest one, we start with it. As we have already said, it is impossible to connect anything when the given list contains only one Posn. Hence, the function just returns MT from the first cond clause. For the second cond clause, let us remind ourselves of what the template expressions compute:

(first p) extracts the first Posn;
(rest p) extracts the NELoP from p; and
(connect-dots (rest p)) renders the NELoP extracted by (rest p) in MT.

From our first attempt to design render-poly, we know that connect-dots needs to add one line to the image that (connect-dots (rest p)) produces, namely, from (first p) to (second p). We know that p contains a second Posn, because otherwise the evaluation of cond would have picked the first clause.

Putting everything together, we get the following definition:

(define (connect-dots p)
  (cond
    [(empty? (rest p)) MT]
    [else
      (render-line
        (connect-dots (rest p)) (first p) (second p))]))

This definition looks simpler than the one for the faulty version of render-poly, even though it has to cope with two more lists of Posns than render-poly.

Our argument that all Polygons are also NELoPs is informal. You will see how to construct a formal argument—called a proof—in a course on sets and/or logic. In general, logic is to computing what analysis is to engineering. Good programmers internalize logic and use it to construct programs that everyone else can easily reason about.

Conversely, we say that connect-dots generalizes render-poly. Every input for the former is also an input for the latter. Or in terms of data definitions, every Polygon is also a NELoP. But there are many NELoPs that are not Polygons. To be precise, all lists of Posns that contain two items or one belong to NELoP but not to Polygon. The key insight for you is, however, that just because a function has to deal with more inputs than another function does not mean that the former is more complex than the latter; generalizations often simplify function definitions.

As spelled out above, the definition of render-polygon can use connect-dots to connect all successive Posns of the given Polygon; to complete its task, it must then add a line from the first to the last Posn of the given Polygon. In terms of code, this just means composing two functions: connect-dots and render-line, but we also need a function to extract the last Posn from the Polygon. Once we are granted this wish, the definition of render-poly is a one-liner:

; Polygon -> Image
; add the Polygon p into an image in MT
(define (render-polygon p)
(render-line (connect-dots p) (first p) (last p)))

Formulating the wish list entry for last is straightforward:

; Polygon -> Posn
; to extract the last Posn on p

Then again, it is clear that last could be a generally useful function and we might be better off designing it for inputs from NELoP:

; NELoP -> Posn
; to extract the last Posn on p
(define (last p)
(first p))

Exercise 175. Argue why it is acceptable to use last on Polygons. Also argue why you may reuse the template for connect-dots for last:
(define (last p)
  (cond
    [(empty? (rest p)) (... (first p) ...)]
    [else (... (first p) ... (last (rest p)) ...)]))
Finally, develop examples for last, turn them into tests, and ensure that the definition of last in figure 47 works on your examples.

(require 2htdp/image)

; A Polygon is one of:
; – (list Posn Posn Posn)
; – (cons Posn Polygon)

(define MT (empty-scene 50 50))

; Polygon -> Image
; add the Polygon p into an image in MT
(define (render-polygon p)
  (render-line (connect-dots p) (first p) (last p)))

; A NELoP is one of:
; – (cons Posn empty)
; – (cons Posn NELoP)

; NELoP -> Image
; connect the Posns in p
(define (connect-dots p)
  (cond
    [(empty? (rest p)) MT]
    [else
      (render-line
        (connect-dots (rest p)) (first p) (second p))]))

; Image Posn Posn -> Image
; draw a red line from Posn p to Posn q into im
(define (render-line im p q)
  (add-line
    im (posn-x p) (posn-y p) (posn-x q) (posn-y q) "red"))

; NELoP -> Posn
; extract the last Posn from p
(define (last p)
  (cond
    [(empty? (rest (rest (rest p)))) (third p)]
    [else (last (rest p))]))
Figure 47: Drawing a polygon

In summary, the development of render-poly naturally points us to consider the general problem of connecting a list of successive dots. We can then solve the original problem by defining a function that composes the general function with other auxiliary functions. The program therefore consists of a relatively straightforward main function—render-poly—and complex auxiliary functions that perform most of the work. You will see time and again that this kind of design approach is common and a good method for designing and organizing programs.

Exercise 176. Here are two more ideas for defining render-poly:
render-poly could cons the last item of p onto p and then call connect-dots.
render-poly could add the first item of p to the end of p via a version of add-at-end that works on Polygons.
Use both ideas to define render-poly; make sure both definitions pass the test cases.

Exercise 177. Modify connect-dots so that it consumes an additional Posn structure to which the last Posn is connected. Then modify render-poly to use this new version of connect-dots. Note: this new version is called an accumulator version.

Naturally, functions such as last are available in a language like Racket and polygon—a function that creates an image of a polygon—is available in one of its libraries ("2htdp/image"). If you are wondering why we just designed a similar function, take a look at the title of the book and the section. The point is not (necessarily) to design useful functions, but to study how programs are designed systematically. Specifically, this section is about the idea of using generalization in the design process, an idea to which the entire part Accumulators is dedicated. }

13 Extended Exercises

This chapter introduces four extended exercises, all of which require and solidify your understanding of the design recipe and the design guidelines. The first one is a batch program; the last three are interactive game programs, which means you are also expected to recall how to design “world” programs.

13.1 Rearranging Words

Newspapers often contain exercises that ask readers to find all possible words made up from some letters. One way to play this game is to form all possible arrangements of the letters in a systematic manner and to see which arrangements are dictionary words. Suppose the letters “a,” “d,” “e,” and “r” are given. There are twenty-four possible arrangements of these letters:

ader
aedr
aerd
adre
arde
ared

daer
eadr
eard
dare
rade
raed

dear
edar
erad
drae
rdae
read

dera
edra
erda
drea
rdea
reda

In this list, there are three legitimate words: “read,” “dear,” and “dare.”

The systematic enumeration of all possible arrangements is clearly a task for a computer program. Let us call the program arrangements.The mathematical term is permutation. and let us agree that it consumes a word and produces a list of the word’s letter-by-letter rearrangements:

; Word -> List-of-words

This basic wish calls for a data definition for Words and then for List-of-words.

One data representation for a word—and the most natural one—is a String. For example, "dear" is an obvious representation for the word dear. A String is an atomic piece of data in BSL+, however, and the very fact that arrangements needs to rearrange the letters in words suggests that String is an inappropriate choice of representation here.

Another data representation of a word is a list of 1Strings where each item in the input represents a letter: "a", "b", ..., "z":

; A Word is either
; – empty or
; – (cons 1String Word)

Exercise 178. Write down the data definition for List-of-words. Systematically make up examples of Words and List-of-words. Finally, formulate the functional example from above with check-expect. Instead of working with the full example, you may wish to start with a word of just two letters, say "d" and "e".

The template of arrangements is that of a list-processing function:

; Word -> List-of-words
; to create a list of all rearrangements of the letters in w
(define (arrangements w)
  (cond
    [(empty? w) ...]
    [else (... (first w) ... (arrangements (rest w)) ...)]))

Not because the output belongs to a collection with a list-shaped data definition but because Word itself is described by a list-shaped data definition.

In preparation of the fifth step, let us look at each cond-line in the template:

If the input is empty, there is only one possible rearrangement of the input: the empty word. Hence the result is (list empty), the list that contains the empty list as the only item.
Otherwise there is a first letter in the word, and (first w) is that letter and the recursion produces the list of all possible rearrangements for the rest of the word. For example, if the list is
(list "d" "e" "r")
then the recursion is (arrangements (list "e" "r")). It will produce the result
(cons (list "e" "r")
(cons (list "r" "e")
empty))
To obtain all possible rearrangements for the entire list, we must now insert the first item, "d" in our case, into all of these words between all possible letters and at the beginning and end.

Our analysis suggests that we can complete arrangements if we can somehow insert one letter a letter into all positions of many different words. The last aspect of this task description implicitly mentions lists and, following the advice of this chapter, calls for an auxiliary function. Let us call this function insert-everywhere/in-all-words and let us use it to complete the definition of arrangements:

(define (arrangements w)
  (cond
    [(empty? w) (list empty)]
    [else (insert-everywhere/in-all-words (first w)
            (arrangements (rest w)))]))

Exercise 179. Design insert-everywhere/in-all-words. It consumes a 1String and a list of words. The result is a list of words like its second argument, but with the first argument inserted at the beginning, between all letters, and at the end of all words of the given list.
Start with a complete wish list entry. Supplement it with tests for empty lists, a list with a one-letter word and another list with a two-letter word, etc. Before you continue, study the following three hints carefully.
Hint 1: Reconsider the example from above. It says that "d" needs to be inserted into the words (list "e" "r") and (list "r" "e"). The following application is therefore one natural candidate for an example and unit test:
(insert-everywhere/in-all-words "d"
  (cons (list "e" "r")
    (cons (list "r" "e")
      empty)))
Keep in mind that the second input corresponds to the sequence of (partial) words “er” and “re”.
Hint 2: You want to use the BSL+ operation append, which consumes two lists and produces the concatenation of the two lists:
> (append (list "a" "b" "c") (list "d" "e"))
(list "a" "b" "c" "d" "e")
the development of functions like append is the subject of section Simultaneous Processing.
Hint 3: This solution of this exercise is a series of functions. Stick to the design recipe and stick to the design guidelines of this chapter. If you can solve the problem, you have understood how to design reasonably complex batch programs.

Exercise 180. Look up the documentation for explode and implode. Then formulate the function arrange-main, which consumes a String and produces all of its possible re-arrangements as a list of Strings.

13.2 Feeding Worms

Worm—also known as Snake—is one of the oldest computer games. When the game starts, a worm and a piece of food appear. The worm is moving toward a wall. Don’t let it run into the wall; otherwise the game is over. Instead, use the arrow keys to control the worm’s movements.

The goal of the game is to have the worm eat as much food as possible. As the worm eats the food, it becomes longer; more and more segments appear. Once a piece of food is digested, another piece appears. The worm’s growth endangers the worm itself, though. As it grows large enough, it can run into itself and, if it does, the game is over, too.

Figure 48: Playing Worm

Figure 48 displays a sequence of screen shots that illustrates how the game works in practice. On the left, you see the initial setting. The worm consists of a single red segment, its head. It is moving toward the food, which is displayed as a green disk. The screen shot in the center shows a situation when the worm is about to eat some food. In the right-most screen shot the worm has run into the right wall. The game is over; the player scored 11 points.

The following exercises guide you through the design and implementation of a Worm game. Like Structures In Lists, these exercises illustrate how to tackle a non-trivial problem via iterative refinement. That is, you don’t design the entire interactive program all at once but in several stages, called iterations. Each iteration adds details and refines the program—until it satisfies you or your customer. If you aren’t satisfied with the outcome of the exercises, feel free to create variations.

Exercise 181. Design an interactive GUI program that continually moves a one-segment worm and enables a player to control the movement of the worm with the four cardinal arrow keys. Your program should use a red disk to render the one-and-only segment of the worm. For each clock tick, the worm should move diameter.
Hints: (1) Re-read section Designing World Programs to recall how to design world programs. When you define the worm-main function, use the rate at which the clock ticks as its argument. See the documentation for on-tick on how to describe the rate. (2) When you develop a data representation for the worm, contemplate the use of two different kinds of representations: a physical representation and a logical one. The physical representation keeps track of the actual physical position of the worm on the screen; the logical one counts how many (widths of) segments the worm is from the left and the top. For which of the two is it easier to change the physical appearances (size of worm segment, size of game box) of the “game?”

Exercise 182. Modify your program from exercise exercise 181 so that it stops if the worm has run into the walls of the world. When the program stops because of this condition, it should render the final scene with the text "worm hit border" in the lower left of the world scene. Hint: You can use the stop-when clause in big-bang to render the last world in a special way. Challenge: Show the worm in this last scene as if it were on its way out of the box.

Exercise 183. Develop a data representation for worms with tails. A worm’s tail is a possibly empty sequence of “connected” segments. Here “connected” means that the coordinates of a segment differ from those of its predecessor in at most one direction and, if rendered, the two segments touch. To keep things simple, treat all segments—head and tail segments—the same.
Then modify your program from exercise 181 to accommodate a multi-segment worm. Keep things simple: (1) your program may render all worm segments as red disks; (2) one way to think of the worm’s movement is to add a segment in the direction in which it is moving and to delete the last segment; and (3) ignore that the worm may run into the wall or into itself.

Exercise 184. Re-design your program from exercise exercise 183 so that it stops if the worm has run into the walls of the world or into itself. Display a message like the one in exercise 182 to explain whether the program stopped because the worm hit the wall or because it ran into itself.
Hint: To determine whether a worm is going to run into itself, check whether the position of the head would coincide with one of its old tail segments if it moved. Hint: Read up on the BSL+ primitive member?.

Exercise 185. Equip your program from exercise 184 with food. At any point in time, the box should contain one piece of food. To keep things simple, a piece of food is of the same size as worm segment. When the worm’s head is located at the same position as the food, the worm eats the food, meaning the worm’s tail is extended by one segment. As the piece of food is eaten, another one shows up at a different location.
Adding food to the game requires changes to the data representation of world states. In addition to the worm, the states now also include a representation of the food, especially its current location. A change to the game representation suggests new functions for dealing with events, though these functions can reuse the functions for the worm (from exercise 184) and their test cases. It also means that the tick handler must not only move the worm; in addition it must manage the eating process and the creation of new food.
Your program should place the food randomly within the box. To do so properly, you need a design technique that you haven’t seen before—so-called generative recursion—so we provide function definitions:For the workings of random, read the manual or exercise 89.
; Posn -> Posn
; ???
(define (food-create p)
(food-check-create p (make-posn (random MAX) (random MAX))))

; Posn Posn -> Posn
; generative recursion
; ???
(define (food-check-create p candidate)
(if (equal? p candidate) (food-create p) candidate))
Before you use them, however, fill in the purpose statements and explain how they work, assuming MAX is greater than 1.
Hints: (1) One way to interpret “eating” is to say that the head moves where the food used to be located and the tail grows by one segment, inserted where the head used to be. Why is this interpretation easy to design as a function? (2) We found it useful to add a second parameter to the worm-main function for this last step, namely, a Boolean that determines whether big-bang displays the current state of the world in a separate window; see the documentation for state on how to ask for this information.

Once you have finished this last exercise, you now have a finished worm game. If you modify your worm-main function so that it returns the length of the final worm’s tail, you can use the “Create Executable” menu in DrRacket to turn your program into something that anybody can launch, not just someone that knows about BSL+ and programming.

You may also wish to add extra twists to the game, to make it really your game. We experimented with funny end-of-game messages; having several different pieces of food around; with extra obstacles in the room; and a few other ideas. What can you think of?

13.3 Simple Tetris

Tetris is another game from the early days of software. Since the design of a full-fledged Tetris game demands a lot of labor with only marginal profit, this section focuses on a simplified version. If you feel ambitious, look up how Tetris really works and design a full-fledged version.

Figure 49: Simple Tetris

In our simplified version, the game starts with individual blocks dropping from the top of the scene. Once it lands on the ground, it comes to a rest and another block starts dropping down from some random place. A player can control the dropping block with the “left” and “right” arrow keys. Once a block lands on the floor of the canvas or on top of some already resting block, it comes to rest and becomes immovable. In a short time, the blocks stack up and, if a stack of blocks reaches the ceiling of the canvas, the game is over. Naturally the objective of this game is to land as many blocks as possible. See figure 49 for an illustration of the idea.

Given this description, we can turn to the design guidelines for interactive programs from Designing World Programs. It calls for separating constant properties from variable ones. The former can be written down as “physical” and graphical constants; the latter suggest the data that makes up all possible states of the world, i.e., the simple Tetris game here. So here are some examples:

The width and the height of the game are fixed as are the blocks. In terms of BSL+, you want definitions like these:

; physical constants
(define WIDTH 10) ; the maximal number of blocks horizontally

; graphical constants
(define SIZE 10) ; blocks are square
(define BLOCK ; they are rendered as red squares with black rims
(overlay (rectangle (- SIZE 1) (- SIZE 1) "solid" "red")
(rectangle SIZE SIZE "outline" "black")))

(define SCENE-SIZE (* WIDTH SIZE))

Explain the last line before you read on.

The “landscape” of resting blocks and the moving block differ from game to game and from clock tick to clock tick. Let us make this more precise. The appearances of the blocks remains the same; their positions differ.

We are now left with the central problem of designing a data representation for the dropping blocks and the landscapes of blocks on the ground. When it comes to the dropping block, there are againSee exercise 181 for a related design decision. two possibilities: one is to choose a “physical” representation, another would be a “logical” one. The physical representation keeps track of the actual physical position of the blocks on the screen; the logical one counts how many block widths a block is from the left and the top. When it comes to the resting blocks, there are even more choices than for individual blocks: a list of physical positions, a list of logical positions, a list of stack heights, etc.

In this section we choose the data representation for you:

; A Tetris is (make-tetris Block Landscape)
; A Landscape is one of:
; – empty
; – (cons Block Landscape)
; Block is (make-block N N)

; interpretation: given (make-tetris (make-block x y) (list b1 b2 ...))
;   (x,y) is the logical position of the dropping block, while
;   b1, b2, etc are the positions of the resting blocks
; a logical position (x,y) determines how many SIZEs the block is
;   from the left—x—and from the top—x.

This is what we dubbed the logical representation, because the coordinates do not reflect the physical location of the blocks, just the number of block sizes they are from the origin. Our choice implies that x is always between 0 and WIDTH (exclusive) and that y is between 0 and HEIGHT (exclusive), but we ignore this knowledge.

Exercise 186. When you are presented with a complex data definition—like the one for the state of a Tetris game—you start by creating instances of the various data collections. Here are some suggestive names for examples you can later use for functional examples:
(define landscape0 ...)
(define block-dropping ...)
(define tetris0 ...)
(define tetris0-drop ...)
...
(define block-landed (make-block 0 (- HEIGHT 1)))
...
(define block-on-block (make-block 0 (- HEIGHT 2)))
Design the program tetris-render, which turns a given instance of Tetris into an Image. Use DrRacket’s interaction area to develop the expression that renders some of your (extremely) simple data examples. Then formulate the functional examples as unit tests and the function itself.

Exercise 187. Design the interactive program tetris-main, which displays blocks dropping in a straight line from the top of the canvas and landing on the floor or on blocks that are already resting. The input to tetris-main should determine the rate at which the clock ticks. See the documentation of on-tick for how to specify the rate.
To discover whether a block landed, we suggest you drop it and check whether it is on the floor or it overlaps with one of the blocks on the list of resting block. Hint: Read up on the BSL+ primitive member?.
When a block lands, your program should immediately create another block that descends on the column to the right of the current one. If the current block is already in the right-most column, the next block should use the left-most one. Alternatively, define the function block-generate, which randomly selects a column different from the current one; see exercise 185 for inspiration.

Exercise 188. Modify the program from exercise 187 so that a player can control the left or right movement of the dropping block. Each time the player presses the "left" arrow key, the dropping block should shift one column to the left unless it is in column 0 or there is already a stack of resting blocks to its left. Similarly, each time the player presses the "right" arrow key, the dropping block should move one column to the right if possible.

Exercise 189. Equip the program from exercise 188 with a stop-when clause. The game ends when one of the columns contains HEIGHT blocks.
It turns out that the design of the stop-when handler is complex. So here are hints: (1) Design a function that consumes a natural number i and creates a column of i blocks. Use the function to define a Landscape for which the game should stop. (2) Design a function that consumes a Landscape and a natural number x0. The function should produce the list of blocks that have the x coordinate x0. (3) Finally, design a function that determines whether the length of any column in some given Landscape is HEIGHT.

Once you have solve exercise 189 you have a bare-bones Tetris game. You may wish to polish it a bit before you show it to your friends. For example, the final screen could show a text that says how many blocks the player was able to stack up. Or every screen could contain such a text. The choice is yours.

13.4 Full Space War

Structure In the World and Itemizations and Structures introduced a simplistic space invader game. It is simplistic because there is little interaction between the ground force and the UFO. Lists And World adds one interesting twist: the player capability to fire as many shots as desired.

The final exercise in this chapter is to design a full-fledged space invader game. As always, a UFO is trying to land on earth. The player’s task is to prevent the UFO from landing. To this end, the game comes with a tank that may fire an arbitrary number of shots. When one of these shots comes close enough to the UFO’s center of gravity, the game is over and the player won. If the UFO comes close enough to the ground, the player lost.

Use the lessons learned from the preceding two sections and design the game slowly, adding one game feature after another. Always use the design recipe and rely on the design guidelines for auxiliary functions. If you like the game, add other features: show a running text; equip the UFO with charges that can harm or eliminate the tank; create an entire fleet of attacking UFOs; and above all, use your imagination.

If you don’t like UFOs and tanks shooting at each other, design an alternative game that has the same organization as the space invader game. Here is one example. You are an airplane flying fire fighter, stationed in the West during the summer and your task is to extinguish fires. And indeed, fires break out everywhere. As the fires grow, they damage the surrounding forests, farms, and towns. You get into your airplane and you drop water charges on these fires to limit the damage. Use an iterative design approach as illustrated in this chapter to create this game.

13.5 Finite State Machines

Finite state machines (FSMs) and regular expressions are ubiquitous elements of programming problems. As A Bit More About Worlds explains, state machines are one possible way to understand and even design world programs. Conversely, exercise 100 shows how to design FSM world programs that determine whether a series of key strokes matches a regular expression.

The solution of exercise 100 is a world program that accepts sequences of key strokes as long as they match this regular expression:

a (b|c)* d

If you wanted a program that recognizes a different pattern, you would need to modify the program in an appropriate manner. The resulting program would closely resemble the original one, and if you were to repeat the same exercise for several different regular expressions, you would end up with may similar programs. A natural thought is to look for a world program that consumes a description of a regular expression and recognizes whether a sequence of key strokes matches the given input. In this section we design such a world program, though we simplify the task a bit and leave the general program as an exercise.

As mentioned every regular expressions corresponds to an FSM, which means that we can focus on designing FSM-consuming programs. Furthermore, we ignore the actual key stroke and have the world transition according to the given FSM for every key stroke. Concerning the imagery, we use FSMs with states that specify colors as string and we display these states as colored squares.

This simplified problem statement dictates the first data definition:

; FSM-State is a String that specifies a color.

Exercise 190. Design the equality predicate state=?; see Input Errors.

Our first data definition also implies how we represent individual transitions in FSMs:

(define-struct transition (current next))
; A Transition is
; (make-transition FSM-State FSM-State)

which, in turn, tells us how to represent a transition table:The * suffix is a notational convention for data definition that deal with lists of items. The next chapter introduces a proper way of saying “list of.”.

; A Transition* is
; – empty
; – (cons Transition Transition*)

We must use a list because we want our world program to work with any FSM and that means a finite, but arbitrary large number of states. Finally, the complete description of an FSM includes its current state, which basically forces us to use the following data definition:

(define-struct fsm (current transitions))
; A FSM is (make-fsm FSM-State Transition*)

Since this definition is complex, we follow the design recipe and create an example:

(define t0
  (list (make-transition "red" "green")
        (make-transition "green" "yellow")
        (make-transition "yellow" "red")))

You probably guessed that this transition table describes a traffic light. Its first transition tells us that the traffic light jumps from "red" to "green", the second one represents the transition from "green" to "yellow", and the last one is for "yellow" to "red". A good starting state for a traffic light is "red":

(define fsm0 (make-fsm "red" t0))

Stop! Why do you think "red" is good for traffic lights?

Exercise 191. The BW Machine is an FSM that flips from black to white and back to black for every key event. Formulate an appropriate transition table and complete FSM.

Now that we have formulated a data definition for the central element of our problem statement, we can follow to the design recipe for world programs. It tells us to differentiate between things that change and things that remain the same over the course of a program evaluation. Given that the main function consumes an instance of FSM, we can ask which parts of this piece of data changes over time and which one is constant. The answer is in the problem statement and says that the FSM’s current state changes for every key stroke; by implication, the transition table stays the same.

This analysis suggests the following data definition

; A SimulationS.v1 is an FSM-State.

According to the design recipe, as applied to the problem statement, this data definition implies the following wish list:

; SimulationS.v1 -> Image
; render a world state as an image
(define (render-state.v1 s)
(square 100 "solid" s))

; SimulationS.v1 -> Image
; given a key stroke ke and current state cs, find the next state
(define (find-next-state.v1 cs ke)
cs)

Since the first wish is so straightforward, we provide the complete function definition. The second wish, however, should cause some consternation. How can find-next-state possibly find the next state when all it is given is the current state and the representation of a key stroke, which according to the problem statement is irrelevant?

What the problem exposes is a fundamental limitation of BSL+ but to appreciate itAlonzo Church and Alan Turing, the first two computer scientists, proved in the 1930s that all programming languages can compute certain functions. Based on this theorem, they conjectured that all programming languages are equal. The first author of this book disagrees and distinguishes the expressive power of programming languages according to how they solve problems. and to explain the work-around, we must proceed to the last step of the world design recipe. Specifically, we must define the main function:

; FSM -> State
; interpret the given finite state machine
(define (simulate.v1 fsm0)
  (big-bang (fsm-current fsm0)
            [to-draw render-state.v1]
            [on-key find-next-state.v1]))

As expected, the function extracts the current state from the given FSM and specifies render-state.v1 as the rendering function and find-next-state.v1 as the key event handler. In the process, the program loses track of the FSM’s transition table, because it neither flows to the rendering function nor the key event handler. By our reasoning above, we should make it a global constant but by the problem statement, the FSM is a parameter of the program’s main function and thus cannot be a global constant.

The next part of the book resolves this conundrum with the introduction of ISL (and ISL+), an extension of the BSL+ programming language. It introduces two new, related linguistic constructs and by using these constructs, the problem disappears. See ... Add Expressive Power.

Here we resolve the problem with a work-around, namely, by using entire FSMs as SimulationSs:

; A SimulationS is an FSM.

This choice means that both the rendering function and the key event handler receive the full FSM, and the latter can use the FSM’s transition table to find the next state. According to the world design recipe, it also means that the key event handler must return an FSM.

Based on this insight, let us work through the world design recipe again, starting with the revised wish list:

; FSM -> Image
; render current world state as a colored square

(check-expect (state-as-colored-square fsm0)
              (square 100 "solid" "red"))

(define (state-as-colored-square fsm)
  (square 100 "solid" (fsm-current fsm)))

; FSM KeyEvent -> FSM
; create an FSM that contains the next state, given that a key
; event took place
(define (find-next-state fsm current)
  fsm)

As before, the rendering function is so straightforward that we simply provide the definition, including a test. In contrast, the key event handler deserves a proper design.

Before we move on, we define the main function:

; FSM -> State
; interpret a given FSM, reacting to each key event with a transition
(define (simulate fsm0)
  (big-bang fsm0
            [to-draw state-as-colored-square]
            [on-key find-next-state]))

The only difference between this definition and the one of simulate.v1 is the initial state of big-bang. Here it is the entire FSM not just the FSM’s current state.

The only remaining task is the design of find-next-state. We have a signature, purpose, and header, so we move on to the example step:

(check-expect (find-next-state fsm0 "n") (make-fsm "green" t0))
(check-expect (find-next-state fsm0 "q") (make-fsm "green" t0))
(check-expect (find-next-state fsm0 "y") (make-fsm "green" t0))

These examples say that no matter what key we press, given fsm0, the next machine representation consists of "green" and the transition table in fsm0. Since the function consumes a structure and a KeyEvent, we write down a template for structures:

(define (find-next-state fsm key-event)
(... (fsm-transitions fsm) .. (fsm-current fsm) ...))

Furthermore, because the desired result is an FSM, we can refine the template as follows:

(define (find-next-state fsm key-event)
(make-fsm ... (fsm-transitions fsm) ... (fsm-current fsm) ...))

The examples suggest that the extracted transition table becomes the second component of the new FSM and that we need both the FSM’s current state and transition table to find the next current state:

(define (find-next-state fsm key-event)
(make-fsm (find (fsm-transitions fsm) (fsm-current fsm))
(fsm-transitions fsm)))

Of course, find is a wish:

; Transition* FSM-State -> FSM-State
; find the state matching current in the transition table

(check-expect (find t0 "red") "green")

(define (find transitions current)
current)

The example for find is derived from the example for find-next-state. Stop! Develop an additional example.

Exercise 192. Complete the design of find. Simulate the traffic FSM specified in fsm0. Also use the complete program to run the BW Machine from exercise 191.

Exercise 193. Our simulation program is quite restrictive. In particular, you cannot use it to represent finite state machines that transition from one state to another when a user presses a specific key event. Revamp the data definition for Transition so that it also specifies the key for which the FSM transitions from one state to the next. Once you have the revised data definition, modify the code so that simulate can deal with these generalized data representations of FSMs.

14 Summary

This second part of the book is about the design of programs that deal with arbitrarily large data. As you can easily imagine, software is particularly useful when it is used on information that comes without pre-specified size limits, meaning “arbitrarily large data” is a critical step on your way to becoming a real programmer. In this spirit, we suggest that you take away three lessons from this part:

It refines the design recipe so that you can deal with self-references and cross-references in data definitions. The occurrence of the former calls for recursive functions, and the occurrence of the latter calls for the use of an auxiliary function and an appropriate call in the main function’s body.
Complex problems call for a decomposition into separate problems and designing a function to solve each of these tasks. The solution to the overall problem is then a function composition. This decomposition-composition design is especially called for when the problem statement implicitly of explicitly mentions auxiliary tasks; when the definition step for a function calls for a traversal of a large or arbitrarily large piece of data; and when a general task is somewhat easier to solve than the specific one in a problem statement.
Pragmatics really matter for program design. Make sure to understand the various clauses you can use in a big-bang description to describe the workings of your “world” programs.

While this part mostly focuses on lists as a good example of arbitrarily large data—because they are practically useful in languages such as Haskell, Lisp, ML, Racket, and Scheme—the ideas apply to all kinds of such data: numbers, files, nested structures, etc. Intertwined Data continues the exploration and demonstrates how the design recipe scales to the most complex kind of data in wide-spread use. In the meantime, the third part takes care of an important worry you should have by now, namely, that a programmer’s work is all about repeating the same steps over and over and over again.

← prev up next →

	Prologue: How to Program
I	Fixed-Size Data
	Intermezzo: BSL
II	Arbitrarily Large Data
	Intermezzo: Quote, Unquote
III	Abstraction
	Intermezzo: Scope
IV	Intertwined Data
	Intermezzo: Pattern Matching
V	Generative Recursion
	Intermezzo: Vectors
VI	Accumulators
	Epilogue

9	Lists
10	Designing With Self-Referential Data Definitions
11	More on Lists
12	Design By Composition
13	Extended Exercises
14	Summary

empty	--- a special value, mostly to represent the empty list
empty?	--- a predicate to recognize empty and nothing else
cons	--- a checked constructor to create two-field instances
first	--- the selector to extract the last item added
rest	--- the selector to extract the extended list
cons?	--- a predicate to recognizes instances of cons

Does the data definition distinguish among different subclasses of data?	Your template needs as many cond clauses as subclasses that the data definition distinguishes.
How do the subclasses differ from each other?	Use the differences to formulate a condition per clause.
Do any of the clauses deal with structured values?	If so, add appropriate selector expressions to the clause.
Does the data definition use self-references?	Formulate ``natural recursions'' for the template to represent the self-references of the data definition.

What are the answers for the non-recursive cond clauses?	The examples should tell you which values you need here. If not, formulate appropriate examples and tests.
What do the selector expressions in the recursive clauses compute?	The data definitions tell you what kind of data these expressions extract and the interpretations of the data definitions tell you what this data represents.
What do the natural recursions compute?	Use the purpose statement of the function to determine what the value of the recursion means not how it computes this answer. If the purpose statement doesn't tell you the answer, improve the purpose statement.
How can you combine these values into the desired answer?	If you are stuck here, arrange the examples from the third step in a table. Place the given input in the first column and the desired output in the last column. In the intermediate columns enter the values of the selector expressions and the natural recursion(s). Add examples until you see a pattern emerge that suggests a ``combinator'' function.

steps	outcome	activity
problem analysis	data definition	identify the information that must be represented; develop a data representation; know how to create data for a specific item of information and how to interpret a piece of data as information; identify self-references in the data definition
header	signature; purpose statement; dummy definition	write down a signature, using the names from the data definitions; formulate a concise purpose statement; create a dummy function that produces a constant value from the specified range
examples	examples and tests	work through several examples, at least one per clause in the (self-referential) data definition; turn them into check-expect tests
template	function template	translate the data definition into a template: one cond clauses per clause; one condition per clause to distinguish the cases; selector expressions per clause if the condition identifies a structure; one natural recursion per self-reference in the data definition
definition	full-fledged definition	find a function that combines the values of the expressions in the cond clauses into the expected answer
test	validated tests	run the tests and validate that they all pass

short-hand	long-hand

(list "ABC")	(cons "ABC" empty)

(list false true)	(cons false (cons true empty))

(list 1 2 3)	(cons 1 (cons 2 (cons 3 empty)))

ader	aedr	aerd	adre	arde	ared

daer	eadr	eard	dare	rade	raed

dear	edar	erad	drae	rdae	read

dera	edra	erda	drea	rdea	reda